题目内容
【题目】如图所示,正方体![]() 的棱长为1,
的棱长为1, ![]() ,
, ![]() 分别是棱
分别是棱![]() ,
, ![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() ,
, ![]() 交于
交于![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,给出以下命题:
,给出以下命题:
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
, ![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]() ,
, ![]() ,则
,则![]() 为常函数;
为常函数;
④若多面体![]() 的体积
的体积![]() ,
, ![]() ,则
,则![]() 为单调函数.
为单调函数.
⑤当![]() 时,四边形
时,四边形![]() 为正方形.
为正方形.
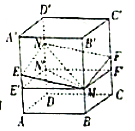
其中假命题的个数为( )
A. 0 B. 3 C. 2 D. 1
【答案】D
【解析】对①,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,同理
,同理![]() ,所以四边形
,所以四边形![]() 为平行四边形,正确;
为平行四边形,正确;
对②因为![]() 平面
平面![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,所以四边形
,所以四边形![]() 面积
面积![]() ,因为
,因为![]() 为定值,所以当
为定值,所以当![]() 分别为
分别为![]() ,
, ![]() 的中点时有最小值,正确;
的中点时有最小值,正确;
对③![]() ,因为
,因为![]() 为定值,
为定值, ![]() 到平面
到平面![]() 的距离为定值,所以
的距离为定值,所以![]() 的体积为定值,即
的体积为定值,即![]() 为常函数,正确;
为常函数,正确;
对④,如图:过![]() 作平面
作平面![]() 平面
平面![]() ,分别交
,分别交![]() ,
, ![]() 于
于![]() ,则多面体
,则多面体![]() 的体积
的体积![]() ,而
,而![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,常数,错;
,常数,错;
对⑤,当![]() 时,四边形
时,四边形![]() 为正方形正确;
为正方形正确;
故选D.

练习册系列答案
相关题目
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?