题目内容
设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn,则x1·x2·…·xn等于 ( ).
A.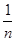 | B.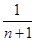 | C.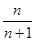 | D.1 |
B
∵f′(x)=(n+1)xn,
∴f′(1)=n+1,
故切线方程为y-1=(n+1)(x-1),
令y=0得切线与x轴交点横坐标xn=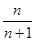 ,
,
∴x1·x2·…·xn=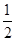 ×
×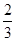 ×…×
×…×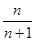 =
=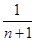
∴f′(1)=n+1,
故切线方程为y-1=(n+1)(x-1),
令y=0得切线与x轴交点横坐标xn=
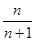 ,
,∴x1·x2·…·xn=
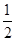 ×
×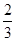 ×…×
×…×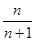 =
=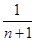

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 x3-
x3-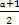 x2+x+b,其中a,b∈R.
x2+x+b,其中a,b∈R.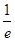
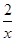 +xln x,则曲线y=f(x)在x=1处的切线方程为( )
+xln x,则曲线y=f(x)在x=1处的切线方程为( )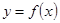 在其图像上任意一点
在其图像上任意一点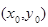 处的切线方程为
处的切线方程为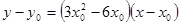 ,且
,且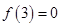 ,则不等式
,则不等式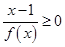 的解集为 .
的解集为 .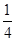
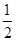
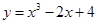 在点
在点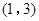 处的切线的斜率为 .
处的切线的斜率为 .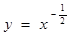 在点
在点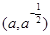 处切线与坐标轴围成的三角形的面积为
处切线与坐标轴围成的三角形的面积为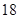 ,则
,则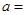 ( )
( )