题目内容
12.设f(x)是一个二次项系数为正的二次函数,f(x+3)=f(-1-x)对任意x∈R都成立,若向量$\overrightarrow{a}$=($\frac{1}{2}$,2sinx),$\overrightarrow{b}$=(2,sinx),$\overrightarrow{c}$=(2,1),$\overrightarrow{d}$=(1,cos2x),求f($\overrightarrow{a}$•$\overrightarrow{b}$)-f($\overrightarrow{c}$•$\overrightarrow{d}$)>0的解集.分析 由已知条件便知二次函数f(x)的对称轴为x=1,并且在[1,+∞)上单调递增,而容易得到$\overrightarrow{a}•\overrightarrow{b}=2-cos2x≥1$,$\overrightarrow{c}•\overrightarrow{d}=2+cos2x≥1$,从而由原不等式可得f(2-cos2x)>f(2+cos2x),这样根据f(x)在[1,+∞)上单调递增便可得出2-cos2x>2+cos2x,从而解该不等式即可得出原不等式的解集.
解答 解:$\overrightarrow{a}•\overrightarrow{b}=1+2si{n}^{2}x=2-cos2x$≥1,$\overrightarrow{c}•\overrightarrow{d}=2+cos2x$≥1;
∵f(x)是一个二次项系数为正的二次函数,f(x+3)=f(-1-x)对任意x∈R都成立;
∴x=1为f(x)的对称轴,f(x)在[1,+∞)上单调递增;
由$f(\overrightarrow{a}•\overrightarrow{b})-f(\overrightarrow{c}•\overrightarrow{d})>0$得,$f(\overrightarrow{a}•\overrightarrow{b})>f(\overrightarrow{c}•\overrightarrow{d})$;
∴f(2-cos2x)>f(2+cos2x);
∴2-cos2x>2+cos2x;
∴cos2x<0;
∴$2kπ+\frac{π}{2}<2x<2kπ+\frac{3π}{2}$,k∈Z;
∴$kπ+\frac{π}{4}<x<kπ+\frac{3π}{4}$,k∈Z;
∴原不等式的解集为$(kπ+\frac{π}{4},kπ+\frac{3π}{4}),k∈Z$.
点评 考查向量数量积的坐标运算,二倍角的余弦公式,余弦函数的值域,以及二次函数的单调性,f(x+m)=f(n-x)时,知道f(x)关于x=$\frac{m+n}{2}$对称,熟悉余弦函数的图象.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | [-2,2] | B. | (-2,2) | C. | $[-2,\sqrt{3})∪({\sqrt{3},2}]$ | D. | $(-2,\sqrt{3})∪(\sqrt{3},2)$ |
| A. | $(0,\frac{1}{2})$ | B. | $[0,\frac{1}{2})$ | C. | $(0,\frac{1}{2}]$ | D. | $[\frac{1}{2},1)$ |
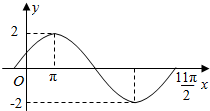 已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$图象的一部分如图所示.
已知函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$图象的一部分如图所示.