题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)若直线![]() 过点
过点![]() 且
且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)已知点![]() ,若直线
,若直线![]() 不与坐标轴垂直,且
不与坐标轴垂直,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)法一:焦点![]() ,当直线
,当直线![]() 斜率不存在时,方程为
斜率不存在时,方程为![]() ,说明不符合题意,故直线的斜率存在,设直线
,说明不符合题意,故直线的斜率存在,设直线![]() 方程为
方程为![]() 与
与![]() 联立得
联立得![]() ,利用韦达定理转化求解
,利用韦达定理转化求解![]() ,求解直线方程.
,求解直线方程.
法二:焦点![]() ,显然直线
,显然直线![]() 不垂直于
不垂直于![]() 轴,设直线
轴,设直线![]() 方程为
方程为![]() ,与
,与![]() 联立得
联立得![]() ,设
,设![]() ,
,![]() ,利用韦达定理以及距离公式,转化求解即可.
,利用韦达定理以及距离公式,转化求解即可.
(2)设![]() ,
,![]() ,设直线
,设直线![]() 方程为
方程为![]() 与
与![]() 联立得:
联立得:![]() ,通过韦达定理以及斜率关系,求出直线系方程,即可推出结果.
,通过韦达定理以及斜率关系,求出直线系方程,即可推出结果.
解:(1)法一:焦点![]() ,
,
当直线![]() 斜率不存在时,方程为
斜率不存在时,方程为![]() ,与抛物线的交点坐标分别为
,与抛物线的交点坐标分别为![]() ,
,![]() ,
,
此时![]() ,不符合题意,故直线的斜率存在.
,不符合题意,故直线的斜率存在.
设直线![]() 方程为
方程为![]() 与
与![]() 联立得
联立得![]() ,
,
当![]() 时,方程只有一根,不符合题意,故
时,方程只有一根,不符合题意,故![]() .
.![]() ,
,
抛物线的准线方程为![]() ,
,
由抛物线的定义得![]()
![]() ,
,
解得![]() ,
,
所以![]() 方程为
方程为![]() 或
或![]() .
.
法二:焦点![]() ,显然直线
,显然直线![]() 不垂直于
不垂直于![]() 轴,设直线
轴,设直线![]() 方程为
方程为![]() ,
,
与![]() 联立得
联立得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() 方程为
方程为![]() 或
或![]() .
.
(2)设![]() ,
,![]() ,
,
设直线![]() 方程为
方程为![]() 与
与![]() 联立得:
联立得:![]() ,
,
可得![]() ,
,![]() .
.
由![]() 得
得![]() ,即
,即![]() .
.
整理得![]() ,即
,即![]() ,
,
整理得![]() ,
,
即![]() ,即
,即![]() .
.
故直线![]() 方程为
方程为![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目
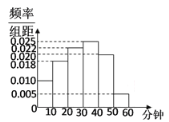
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为体育迷.若抽取100人中有女性55人,其中女体育迷有10人,完成答题卡中的列联表并判断能否在犯错误概率不超过0.05的前提下认为体育迷与性别有关系?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附表及公式: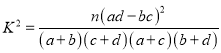 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |