题目内容
【题目】若函数
的图象与曲线C:
存在公共切线，则实数
的取值范围为
A. 
B. 
C. 
D. 
【答案】A
【解析】
设公切线与f（x）、g（x）的切点坐标，由导数的几何意义、斜率公式列出方程化简，分离出a后构造函数，求出函数的最值，即可求出实数a的取值范围．
设公切线与f（x）＝x2+1的图象切于点（x1，
），
与曲线C：g（x）＝aex+1切于点（x2，
），
∴2x1＝
＝
，
化简可得，2x1＝
，得x1＝0或2x2＝x1+2，
∵2x1＝，且a＞0，∴x1＞0，则2x2＝x1+2＞2，即x2＞1，
由2x1＝
得a＝
，
设h（x）＝
（x＞1），则h′（x）＝
，
∴h（x）在（1，2）上递增，在（2，+∞）上递减，
∴h（x）max＝h（2）＝
，
∴实数a的取值范围为（0，]，
故选：A．
【题目】目前，新冠病毒引发的肺炎疫情在全球肆虐，为了解新冠肺炎传播途径，采取有效防控措施，某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息，数据经过汇总整理得到如图所示的频率分布直方图（用频率作为概率）.潜伏期不高于平均数的患者，称为“短潜伏者”，潜伏期高于平均数的患者，称为“长潜伏者”.
（1）求这500名患者潜伏期的平均数（同一组中的数据用该组区间的中点值作代表），并计算出这500名患者中“长潜伏者”的人数；
（2）为研究潜伏期与患者年龄的关系，以潜伏期是否高于平均数为标准进行分层抽样，从上述500名患者中抽取300人，得到如下表格.
（i）请将表格补充完整；
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
（ii）研究发现，某药物对新冠病毒有一定的抑制作用，现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验，再从选取的7人中随机抽取两人做Ⅱ期临床试验，求两人中恰有1人为“长潜伏者”的概率.
【题目】《中华人民共和国道路交通安全法》第47条的相关规定：机动车行经人行横道时，应当减速慢行；遇行人正在通过人行横道，应当停车让行，俗称“礼让斑马线”，《中华人民共和国道路交通安全法》 第90条规定：对不礼让行人的驾驶员处以扣3分，罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据：
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
（1）请利用所给数据求违章人数y与月份之间的回归直线方程
+
（2）预测该路口7月份的不“礼让斑马线”违章驾驶员人数；
（3）交警从这5个月内通过该路口的驾驶员中随机抽查了50人，调查驾驶员不“礼让斑马线”行为与驾龄的关系，得到如下2
列联表：
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
能否据此判断有97.5
的把握认为“礼让斑马线”行为与驾龄有关？
参考公式及数据：
,
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（其中n=a+b+c+d）
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动，治疗特种病的创新药研发成了当务之急．为此，某药企加大了研发投入，市场上治疗一类慢性病的特效药品
的研发费用
（百万元）和销量
（万盒）的统计数据如下：
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
（1）求与的相关系数
精确到0.01，并判断与的关系是否可用线性回归方程模型拟合？（规定：
时，可用线性回归方程模型拟合）；
（2）该药企准备生产药品的三类不同的剂型
，
，
，并对其进行两次检测，当第一次检测合格后，才能进行第二次检测．第一次检测时，三类剂型，，合格的概率分别为
，
，
，第二次检测时，三类剂型，，合格的概率分别为，，
．两次检测过程相互独立，设经过两次检测后，，三类剂型合格的种类数为
，求的数学期望．
附：（1）相关系数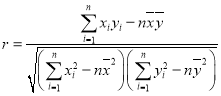
（2）
，
，
，
．