题目内容
【题目】已知函数
．
（1）若
在
处导数相等，证明：
为定值，并求出该定值；
（2）已知对于任意
，直线
与曲线
有唯一公共点，求实数
的取值范围.
【答案】（1）6；（2）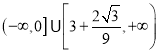
【解析】
（1）求出原函数的导函数，结合在
处导数相等及根与系数的关系可得
，从而求得
为定值6；（2）由
，可知函数
在
的图象为下凸，在
的图象为上凸，求得函数的极大值点
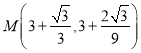，再由直线
过点
，然后对
分类讨论求使直线与曲线
有唯一公共点的实数的取值范围．
（1）证明：
，
，
由题意得，，
则
；
（2）解：
，
函数在的图象为下凸，在的图象为上凸，
记
，求得
处的切线为
，再记
，
由
，求得的极大值点为，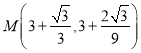
①当
时，直线与曲线显然只有唯一公共点；
②当
时，直线
斜率为正，且与曲线有三个公共点，舍去；
③当
时，直线
斜率为正，且与曲线有三个公共点，舍去；
④当
时，若
，在直线上方，直线与曲线的上凸部分有唯一公共点，与下凸部分不相交；
若
，直线与曲线）交于P点，与上凸部分和下凸部分均不相交；
若
，在直线下方，直线y=kx+a与曲线的下凸部分有唯一公共点，与上凸部分不相交，此种情况成立．
综上，的取值范围为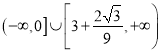
．
练习册系列答案
相关题目
