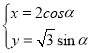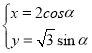题目内容
【题目】给出以下四个命题：
①数列
为等差数列的充要条件是其通项公式为n的一次函数.
②在面积为S的
的边AB上任取一点P，则
的面积大于
的概率为
.
③将多项式
分解因式得
，则
.
④若那么由
，那么由
以及x轴所围成的图形一定在x轴下方.
其中正确命题的序号为_____________（把所有正确命题的序号都填上）
【答案】②③
【解析】
举例说明①④错误；由几何概型求概率说明②正确；由二项式系数的性质求得
说明③正确.
常数列也是等差数列，但常数列的通项公式为常数函数，不是n的一次函数，故①错误;
根据几何概型可知，
的面积大于
的概率为
，故②正确;
由二项展开式的通项公式可得, 
中
的系数为
，
的系数为
，则
，故③正确；
以及
轴所围成的图形可能一部分在x轴下方, 一部分在x轴上方. 如
由
以及x轴所围成的图形如图:
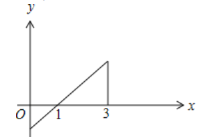
故④错误.
故答案为：②③
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案【题目】“网购”已经成为我们日常生活中的一部分，某地区随机调查了100名男性和100名女性在“双十一”活动中用于网购的消费金额，数据整理如下：
男性消费金额频数分布表
消费金额 （单位：元） | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人数 | 15 | 15 | 20 | 30 | 20 |
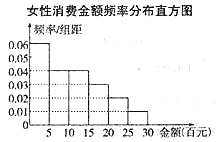
（1）试分别计算男性、女性在此活动中的平均消费金额；
（2）如果分别把男性、女性消费金额与中位数相差不超过200元的消费称作理性消费，试问是否有5成以上的把握认为理性消费与性别有关.
附：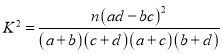
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
【题目】数据的收集和整理在当今社会起到了举足轻重的作用，它用统计的方法来帮助人们分析以往的行为习惯，进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员，他收集到了甲、乙两名球员近期5场比赛的传球成功次数，如下表：
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
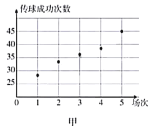
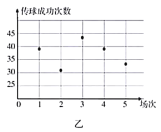
（1）根据这两名球员近期5场比赛的传球成功次数，完成茎叶图（茎表示十位，叶表示个位）；分别在平面直角坐标系中画出两名球员的传球成功次数的散点图；
（2）求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差；
（3）主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平，同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.
