题目内容
【题目】足球运动是一项古老的体育活动,众多的资料表明,中国古代足球的出现比欧洲早,历史更为悠久,如图,现代比赛用足球是由正五边形与正六边形构成的共32个面的多面体,著名数学家欧拉证明了凸多面体的面数(F),顶点数(V),棱数(E)满足F+V-E=2,那么,足球有______.个正六边形的面,若正六边形的边长为![]() ,则足球的直径为______.cm(结果保留整数)(参考数据
,则足球的直径为______.cm(结果保留整数)(参考数据![]()

【答案】20 22
【解析】
首先根据足球表面的规律,设正五边形为![]() 块,正六边形为
块,正六边形为![]() 块,列出方程组
块,列出方程组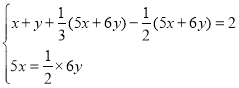 ,解方程组即可.分别计算正六边形和正五边形的面积,从而得到足球的表面积,再利用球体表面积公式即可得到足球的直径.
,解方程组即可.分别计算正六边形和正五边形的面积,从而得到足球的表面积,再利用球体表面积公式即可得到足球的直径.
因为足球是由正五边形与正六边形构成,
所以每块正五边形皮料周围都是正六边形皮料,
每两个相邻的多边形恰有一条公共边,每个顶点处都有三块皮料,
而且都遵循一个正五边形,两个正六边形结论.
设正五边形为![]() 块,正六边形为
块,正六边形为![]() 块,有题知:
块,有题知:
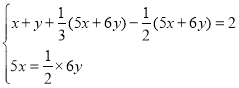 ,解得
,解得![]() .
.
所以足球有![]() 个正六边形的面.
个正六边形的面.
每个正六边形的面积为![]() .
.
每个正五边形的面积为![]() .
.
球的表面积![]()
![]() .
.
所以![]() ,
,![]() .
.
所以足球的直径为![]() .
.
故答案为:![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目