题目内容
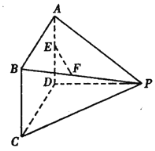
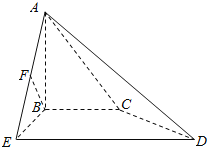
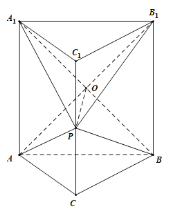
【题目】如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠ABC=45°,AB=AA1=2,P为CC1的中点.
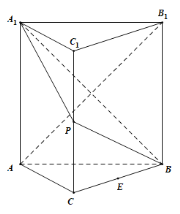
(1)证明:AB1⊥平面PA1B;
(2)设E为BC的中点,线段AB1上是否存在一点Q,使得QE∥平面A1ACC1?若存在,求四棱锥Q﹣AA1C1C的体积;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在;体积![]()
【解析】
解法一:(1)证明A1ABB1为正方形,设A1B交AB1于点O,则O为AB1的中点,且A1B⊥AB1.
连接PA,PB1,PO,推出PO⊥AB1,然后证明AB1⊥平面PA1B.
(2)当Q为AB1中点,即点Q与点O重合时,QE∥平面A1ACC1.连接A1C,说明QE∥平面AA1C1C.Q到平面A1ACC1的距离等于B到平面A1ACC1的距离的一半,转化求解几何体的体积即可.
解法二:(1)证明A1ABB1为正方形,设A1B交AB1于点O,则O为AB1的中点,且A1B⊥AB1.连接B1C交BP于F点,推出BB1⊥平面ABC,AC⊥BB1.结合AC⊥BC,证明AC⊥平面BB1C1C,证明BP⊥平面AB1C,然后证明A1B⊥平面PA1B.
(2)当Q为AB1中点,即点Q与点O重合时,QE∥平面A1ACC1.
取AB中点M,连接QM,ME,说明Q到平面A1ACC1的距离等于E到平面A1ACC1的距离,利用等体积法![]() 转化求解即可.
转化求解即可.
解法三:(1)设A1B交AB1于点O,说明A1ABB1为正方形,
得到A1B⊥AB1,连接PA,PB1,PO,推出PO⊥AB1,证明PO⊥平面ABB1A1.得到平面PA1B⊥平面ABB1A1.即可证明AB1⊥平面PA1B.(2)同方法一
解:解法一:(1)证明:在△ABC中,
∵∠ACB=90°,∠ABC=45°,AB=2,
∴![]() ,
,
又直三梭柱ABC﹣A1B1C1中,AB=AA1=2,则A1ABB1为正方形,
设A1B交AB1于点O,则O为AB1的中点,且A1B⊥AB1.
连接PA,PB1,PO,

∵侧棱CC1⊥底面ABC,P为CC1的中点,则![]() ,
,![]() ,
,
故PA=PB1.
∴PO⊥AB1,
∵PO∩A1B=O,且PO,A1B平面PA1B,
∴AB1⊥平面PA1B.
(2)当Q为AB1中点,即点Q与点O重合时,QE∥平面A1
理出如下:
连接A1C,∵E为BC的中点,∴则QE∥A1C,
∵QE平面AA1C1C,A1C平面AA1C1C,
∴QE∥平面AA1C1C.
此时,Q到平面A1ACC1的距离等于B到平面A1ACC1的距离的一半,
又![]() ,
,
∴![]() .
.
解法二:(1)证明:在△ABC中,∵∠ACB=90°,∠ABC=45°,AB=2,
∴![]() ,
,
又直三棱柱ABC﹣A1B1C1中,AB=AA1=2,则A1ABB1为正方形,
设A1B交AB1于点O,则O为AB1的中点,且A1B⊥AB1.
连接B1C交BP于F点,在直三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,
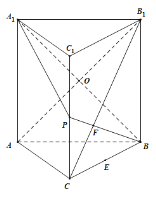
∵AC平面ABC,∴AC⊥BB1.
又AC⊥BC,BC∩BB1=B,BC,BB1平面BB1C1C,
∴AC⊥平面BB1C1C,
∵BP平面BB1C1C,∴AC⊥BP,
在矩形BB1C1C中,P为CC1的中点,则![]() ,
,![]() ,
,
由CC1∥BB1得△CPF∽△BB1F,∴![]() ,
,
∴![]() ,
,![]() ,∴PF2+CF2=PC2,故B1C⊥PB,
,∴PF2+CF2=PC2,故B1C⊥PB,
又AC⊥BP,AC∩B1C=C,AC,B1C平面AB1C,∴BP⊥平面AB1C,
∵AB1平面AB1C,∴AB1⊥BP.
又A1B⊥AB1,A1B∩BP=B,A1B,BP平面PA1B,∴A1B⊥平面PA1B.
(2)当Q为AB1中点,即点Q与点O重合时,QE∥平面A1ACC1.
理由如下:
取AB中点M,连接QM,ME,又CE=BE,∴ME∥AC,

∵ME平面A1ACC1,AC平面A1ACC1,
∴ME∥平面A1ACC1.
同理可得QM∥平面A1ACC1.
又∵ME∩QM=M,ME,QM平面QME,
∴平面QME∥平面A1ACC1,
又∵QE平面QME,
∴QE∥平面A1ACC1.
此时,Q到平面A1ACC1的距离等于E到平面A1ACC1的距离,
在直三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,
∵BC平面ABC,∴CC1⊥BC,
又AC⊥BC,AC∩CC1=C,AC,CC1平面AA1C1C,∴BC⊥平面AA1C1C,
∴EC为四棱锥Q﹣AA1C1C的高,![]() .
.
∴![]() .
.
解法三:(1)证明:在△ABC中,
∵∠ACB=90°,∠ABC=45°,AB=2,
∴![]() ,
,
设A1B交AB1于点O,
在直三棱柱ABC﹣A1B1C1中,AA1=2,A1ABB1为正方形,
∴O为AB1中点,且A1B⊥AB1.
连接PA,PB1,PO,
∵侧棱CC1⊥底面ABC,P为CC1的中点,则![]() ,
,![]() ,
,
故PA=PB1.
∴PO⊥AB1,
同理可得PO⊥A1B.
又A1B∩AB1=O,A1B,AB1平面ABB1A1,PO⊥平面ABB1A1.
∵PO平面PA1B,
∴平面PA1B⊥平面ABB1A1.
∵平面PA1B∩平面ABB1A1=A1B,AB1平面ABB1A1,
∴AB1⊥平面PA1B.
(2)同方法一

 优生乐园系列答案
优生乐园系列答案【题目】数据的收集和整理在当今社会起到了举足轻重的作用,它用统计的方法来帮助人们分析以往的行为习惯,进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员,他收集到了甲、乙两名球员近期5场比赛的传球成功次数,如下表:
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
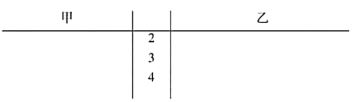
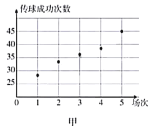
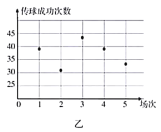
(1)根据这两名球员近期5场比赛的传球成功次数,完成茎叶图(茎表示十位,叶表示个位);分别在平面直角坐标系中画出两名球员的传球成功次数的散点图;
(2)求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差;
(3)主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平,同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.