题目内容
已知f(x)=3x,f(a+2)=27,函数g(x)=λ•2ax-4x的定义域为[0,2]
(1)求a的值
(2)若函数g(x)的最大值是
,求实数λ的值.
(1)求a的值
(2)若函数g(x)的最大值是
| 1 |
| 3 |
(1)依题f(a+2)=3a+2=27,
解之得a+2=3,得a=1--------------------------------------------(2分)
(2)令2x=t,由0≤x≤2,可得t∈[1,4]-------------------------(4分)
g(x)=h(t)=-t2+λt=-(t-
λ)2+
λ2.t∈[1,4]
①当
λ<1即λ<2时,[h(t)]max=h(1)=λ-1=
,
解得λ=
,符合条件-------------------------(8分)
②当1≤
λ<4,即2≤λ<8时,[h(t)]max=h(
λ)=
λ2=
解之得λ=±
∉[2,8),不符合题意,舍去----(9分)
③当
λ≥4,即λ≥8时,[h(t)]max=h(4)=4λ-16=
解之得λ=
<8,不符合题意,舍去------------------(11分)
综上所述,函数g(x)的最大值是
时,实数λ的值
.---------------------------(12分)
解之得a+2=3,得a=1--------------------------------------------(2分)
(2)令2x=t,由0≤x≤2,可得t∈[1,4]-------------------------(4分)
g(x)=h(t)=-t2+λt=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
①当
| 1 |
| 2 |
| 1 |
| 3 |
解得λ=
| 4 |
| 3 |
②当1≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
解之得λ=±
2
| ||
| 3 |
③当
| 1 |
| 2 |
| 1 |
| 3 |
解之得λ=
| 49 |
| 12 |
综上所述,函数g(x)的最大值是
| 1 |
| 3 |
| 4 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
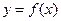 的值域是
的值域是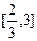 ,则函数
,则函数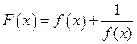 的值域
的值域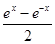 ,x∈R
,x∈R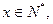
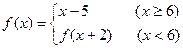 ,则
,则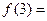
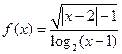 的定义域为 .
的定义域为 .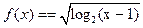 的定义域为A,集合
的定义域为A,集合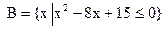 ,
,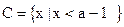 (1)求
(1)求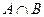 ; (2)若
; (2)若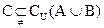 ,求
,求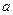 的取值范围。
的取值范围。