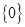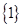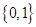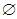题目内容
函数f(x)=2x+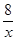 (x>0)有
(x>0)有
| A.最大值8 | B.最小值8 | C.最大值4 | D.最小值4 |
B
解析试题分析:因为均值不等式中,两个数的几何平均数小于等于两个正数的算术平均数,因此得到f(x)=2x+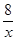 (x>0)
(x>0)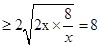 当且仅当
当且仅当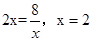 ,时取得等号,故选B.
,时取得等号,故选B.
考点:函数的最值
点评:解决该试题的函数最值,可以运用函数的单调性,也可以运用均值不等式来得到,属于基础题。

练习册系列答案
相关题目
下表表示y是x的函数,则函数的值域是( )
| x | 0<x<5 | 5≤x<10 | 10≤x<15 | 15≤x≤20 |
| y | 2 | 3 | 4 | 5 |
已知定义域为 的偶函数
的偶函数 在
在 上是减函数,且
上是减函数,且 ,则不等式
,则不等式 ( )
( )
A. | B. | C. | D. |
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=
| A.-3 | B.-1 | C.1 | D.3 |
若存在实数x∈[2,4],使x2-2x+5-m<0成立,则m的取值范围为
| A.(13,+∞) | B.(5,+∞) | C.(4,+∞) | D.(-∞,13) |
已知函数 满足
满足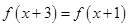 ,且
,且 ∈[-1,1]时,
∈[-1,1]时,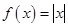 ,则函数
,则函数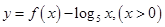 的零点个数是( )
的零点个数是( )
| A.3 | B.4 | C.5 | D.6 |
已知函数 中,常数
中,常数 那么
那么 的解集为
的解集为
A.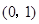 | B. | C. | D. |
已知函数 ,,则函数
,,则函数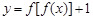 的零点个数是
的零点个数是
| A.4 | B.3 | C.2 | D.1 |
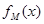 的定义域为R,且定义如下:
的定义域为R,且定义如下: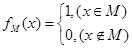 (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足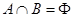 ,则函数
,则函数 的值域为 ( )
的值域为 ( )