题目内容
已知二次函数f(x)=ax2+2x+c(a≠0)的图象与y轴交于点(0,1),且满足f(-2+x)=f(-2-x)(x∈R)
(Ⅰ)求该二次函数的解析式及函数的零点.
(Ⅱ)已知函数在(t-1,+∞)上为增函数,求实数t的取值范围.
(Ⅰ)求该二次函数的解析式及函数的零点.
(Ⅱ)已知函数在(t-1,+∞)上为增函数,求实数t的取值范围.
(I)因为二次函数f(x)=ax2+2x+c(a≠0)的图象与y轴交于点(0,1),所以c=1
又因为函数f(x)满足f(-2+x)=f(-2-x)(x∈R),所以x=-
=-2,所以a=
所以二次函数的解析式为:f(x)=
x2+2x+1
由f(x)=0,可得函数的零点为:-2+
,-2-
;
(II)因为函数在(t-1,+∞)上为增函数,且函数图象的对称轴为x=-2,
所以由二次函数的图象可知:t-1≥-2
∴t≥-1.
又因为函数f(x)满足f(-2+x)=f(-2-x)(x∈R),所以x=-
| 2 |
| 2a |
| 1 |
| 2 |
所以二次函数的解析式为:f(x)=
| 1 |
| 2 |
由f(x)=0,可得函数的零点为:-2+
| 2 |
| 2 |
(II)因为函数在(t-1,+∞)上为增函数,且函数图象的对称轴为x=-2,
所以由二次函数的图象可知:t-1≥-2
∴t≥-1.

练习册系列答案
相关题目
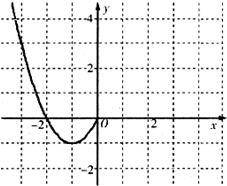
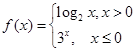 ,且函数
,且函数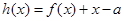 有且只有一个零点,则实数
有且只有一个零点,则实数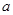 的取值范围是( )
的取值范围是( )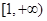 B.
B.
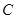 .
.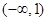 D.
D.