题目内容
函数f（x）=2x2-mx+3，当x∈[2，+∞）时是增函数，当x∈（-∞，2]时是减函数，则f（1）=______．
函数f（x）=2x2-mx+3的对称轴为x=-
=
．
∵当x∈[2，+∞）时是增函数，当x∈（-∞，2]时是减函数，
∴x=2是函数f（x）=2x2-mx+3的对称轴，
即
=2，解得m=8．
∴f（x）=2x2-8x+3，
即f（1）=2-8+3=-3．
故答案为：-3．
| -m |
| 2×2 |
| m |
| 4 |
∵当x∈[2，+∞）时是增函数，当x∈（-∞，2]时是减函数，
∴x=2是函数f（x）=2x2-mx+3的对称轴，
即
| m |
| 4 |
∴f（x）=2x2-8x+3，
即f（1）=2-8+3=-3．
故答案为：-3．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
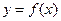的图象经过三点
。
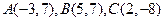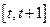上的最大值和最小值。
的解集是 ．