题目内容
已知函数f（x）=2x2+（x-a）2．
（Ⅰ）若f（x+1）为偶函数，求a的值；
（Ⅱ）若f（x）在[0，1]上有最小值9，求a的值．
（Ⅰ）若f（x+1）为偶函数，求a的值；
（Ⅱ）若f（x）在[0，1]上有最小值9，求a的值．
（Ⅰ）f（x）=2x2+（x-a）2=3x2-2ax+a2
∵函数f（x+1）为偶函数，∴二次函数函数f（x）的对称轴为x=1．----------（2分）
∴直线x=
即直线x=1，解之得a=3；-----------------（4分）
（Ⅱ）f（x）=2x2+（x-a）2=3x2-2ax+a2
函数图象关于直线x=
对称
①当
＜0即a＜0时，函数在[0，1]上为增函数，可得
最小值为fmin(x)=f(0)=a2=9，解之得a=-3------------（6分）
②当0≤
≤1即0≤a≤1时，函数最小值为fmin(x)=f(
)=
a2=9，矛盾----------（8分）
③当
＞1即a＞1时，函数在[0，1]上为减函数，可得
最小值为fmin(x)=f(1)=3-2a+a2=9，解之得a=1+
（舍负）----------（10分）
综上所述，满足条件的a值为-3或a=1+
．--------------------------（12分）
∵函数f（x+1）为偶函数，∴二次函数函数f（x）的对称轴为x=1．----------（2分）
∴直线x=
| a |
| 3 |
（Ⅱ）f（x）=2x2+（x-a）2=3x2-2ax+a2
函数图象关于直线x=
| a |
| 3 |
①当
| a |
| 3 |
最小值为fmin(x)=f(0)=a2=9，解之得a=-3------------（6分）
②当0≤
| a |
| 3 |
| a |
| 3 |
| 2 |
| 3 |
③当
| a |
| 3 |
最小值为fmin(x)=f(1)=3-2a+a2=9，解之得a=1+
| 7 |
综上所述，满足条件的a值为-3或a=1+
| 7 |
练习册系列答案
名校课堂系列答案
相关题目
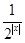＋2.