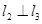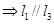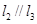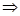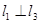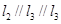题目内容
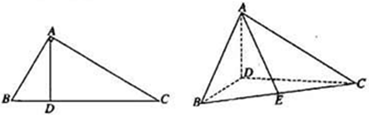
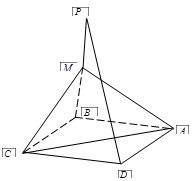
如右图,在四棱锥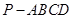 中,底面
中,底面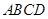 为平行四边形,
为平行四边形,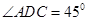 ,
,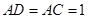 ,
,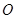 为
为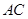 中点,
中点,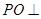 平面
平面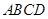 ,
, 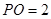 ,
,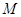 为
为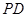 中点.
中点.
(1)证明: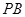 //平面
//平面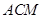 ;
;
(2)证明: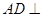 平面
平面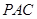 ;
;
(3)求直线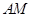 与平面
与平面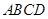 所成角的正切值.
所成角的正切值.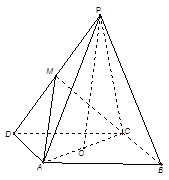
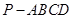 中,底面
中,底面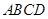 为平行四边形,
为平行四边形,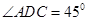 ,
,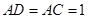 ,
,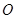 为
为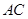 中点,
中点,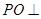 平面
平面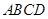 ,
, 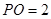 ,
,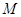 为
为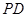 中点.
中点.(1)证明:
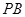 //平面
//平面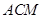 ;
;(2)证明:
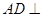 平面
平面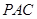 ;
;(3)求直线
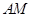 与平面
与平面 所成角的正切值.
所成角的正切值.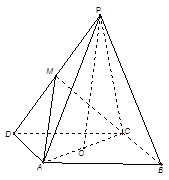
(1)证明:见解析;(2)证明:见解析;(3)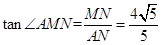
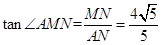
本题考查线面平行、线面垂直、面面垂直,解题的关键是正确运用线面平行、线面垂直、面面垂直的判定定理,属于中档题.
(Ⅰ)证明PB∥平面ACM,利用线面平行的判定定理,证明MO∥PB即可;
(Ⅱ)证明AD⊥平面PAC,利用线面垂直的判定定理,证明AD⊥AC,AD⊥PO即可;
(Ⅲ)根据AD⊥平面PAC,利用面面垂直的判定定理,可证平面PAD⊥平面PAC,从而得到线面角的求解。
(1)证明:连接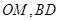
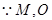 分别为
分别为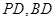 中点,
中点,
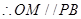
又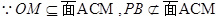
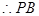 //平面
//平面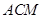
(2)证明: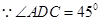 ,
,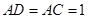
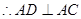

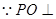 平面
平面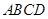 ,且
,且
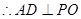
又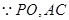 为平面
为平面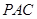 内的两条相交直线
内的两条相交直线
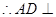 平面
平面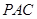
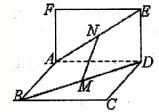
(3)解:作OD中点N,连接MN,AN
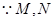 分别为
分别为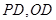 中点
中点

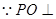 平面
平面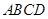
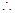
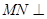 平面
平面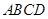
即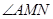 为直线
为直线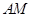 与平面
与平面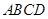 所成角
所成角
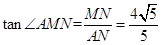
(Ⅰ)证明PB∥平面ACM,利用线面平行的判定定理,证明MO∥PB即可;
(Ⅱ)证明AD⊥平面PAC,利用线面垂直的判定定理,证明AD⊥AC,AD⊥PO即可;
(Ⅲ)根据AD⊥平面PAC,利用面面垂直的判定定理,可证平面PAD⊥平面PAC,从而得到线面角的求解。
(1)证明:连接
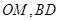
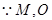 分别为
分别为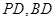 中点,
中点,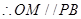
又
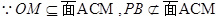
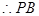 //平面
//平面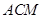
(2)证明:
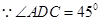 ,
,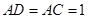
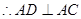

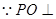 平面
平面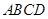 ,且
,且
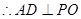
又
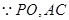 为平面
为平面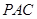 内的两条相交直线
内的两条相交直线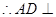 平面
平面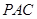
(3)解:作OD中点N,连接MN,AN
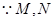 分别为
分别为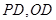 中点
中点
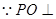 平面
平面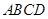
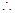
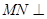 平面
平面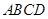
即
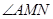 为直线
为直线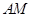 与平面
与平面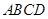 所成角
所成角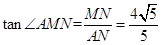

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
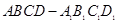 中,
中,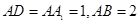 ,点E是AB的中点.
,点E是AB的中点.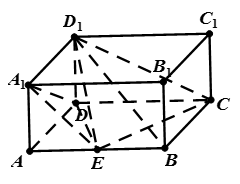
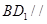 平面
平面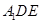 ;
;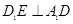 ;
;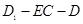 的正切值.
的正切值.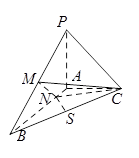
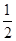 AB,
AB,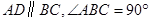 ,
,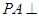 平面
平面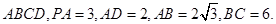
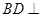 平面PAC;
平面PAC;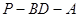 的大小.
的大小.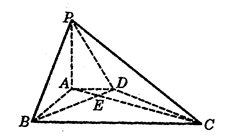
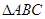 中,
中,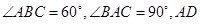 是
是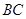 上的高,沿
上的高,沿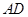 把
把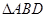 折起,使
折起,使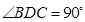 。
。
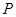 为平行四边形
为平行四边形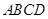 所在平面外一点,
所在平面外一点,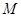 为
为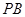 的中点,
的中点,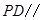 平面
平面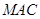 .
.
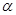 ,则b与
,则b与 平面
平面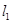 ,
,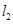 ,
,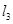 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )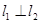 ,
,