题目内容
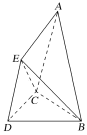
【题目】四棱锥S-ABCD的底面为正方形,SD![]() 底面ABCD如下列结论中不正确的是 。
底面ABCD如下列结论中不正确的是 。
A. AB![]() SA
SA
B. BC//平面SAD
C. BC与SA所成的角等于AD与 SC所成的角
D. SA与平面SBD所成的角等于SC与平面SBD所成的角
【答案】C
【解析】
因为根据SD⊥底面ABCD,底面ABCD为正方形,以及三垂线定理,易证AC⊥SB,根据线面平行的判定定理易证AB∥平面SCD,,根据直线与平面所成角的定义,可以找出∠SAD是SA与平面SBD所成的角,∠SCD是SC与平面SBD所成的角,根据三角形全等,证得这两个角相等;异面直线所成的角,利用线线平行即可求得结果.∵SD⊥底面ABCD,
∠SAD是SA与平面SBD所成的角,∠SCD是SC与平面SBD所成的角,
而△SAD≌△SBD,∴∠SAD=∠SCD,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故D正确;A,B,C不正确。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的![]() 缴纳,
缴纳,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y(单位:元)与年份序号t的统计如下表:
(1)求出t关于t的线性回归方程![]() ;
;
(2)试预测2019年该员工的月平均工资为多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(注: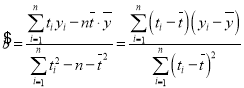 ,
,![]() ,其中
,其中![]() )
)