题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,则
,则![]() 的面积的最大值为
的面积的最大值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
解三角形,建立坐标系,设AD斜率为k,用k表示出B′纵坐标,代入面积公式得出面积关于k的函数,根据k的范围和函数单调性求出面积最大值.
由余弦定理可得AC2=AB2+BC2﹣2ABBCcosB=12+9﹣2×2![]() 3
3![]() 3,
3,
∴AC![]() ,且AC2+BC2=AB2,
,且AC2+BC2=AB2,
∴AC⊥BC,
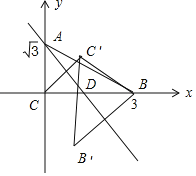
以C为原点,以CB,CA为坐标轴建立平面直角坐标系,如图所示:
设直线AD的方程为y=kx![]() ,
,
当D与线段AB的端点重合时,B,B',C'在同一条直线上,不符合题意,
∴则k![]() ,设B′(m,n),显然n<0,
,设B′(m,n),显然n<0,
则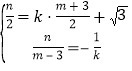 ,解得n
,解得n![]() ,
,
∵CC′∥BB′,
∴S△BB′C′=S△BB′C![]() ,
,
令f(k)![]() (k
(k![]() ),则f′(k)
),则f′(k)![]() ,
,
令f′(k)=0可得k![]() 或k
或k![]() (舍),
(舍),
∴当k![]() 时,f′(k)>0,当
时,f′(k)>0,当![]() k
k![]() 时,f′(k)<0,
时,f′(k)<0,
∴当k![]() 时,f(k)取得最大值f(
时,f(k)取得最大值f(![]() )
)![]() .
.
故选:D.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)