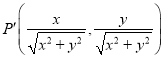题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为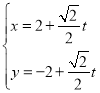 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)在直线![]() 的参数方程中消去
的参数方程中消去![]() ,可得出直线
,可得出直线![]() 的普通方程,由
的普通方程,由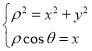 可将曲线
可将曲线![]() 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(2)设点![]() ,求出直线
,求出直线![]() 的普通方程,利用点到直线的距离公式结合三角恒等变换思想以及正弦函数的有界性可求得点
的普通方程,利用点到直线的距离公式结合三角恒等变换思想以及正弦函数的有界性可求得点![]() 到直线
到直线![]() 距离的最大值,进而可求得
距离的最大值,进而可求得![]() 面积的最大值.
面积的最大值.
(1)直线![]() 的参数方程为
的参数方程为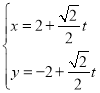 (
(![]() 为参数),消去参数
为参数),消去参数![]() 得
得![]() ,
,
所以,直线![]() 的普通方程为
的普通方程为![]() .
.
曲线![]() 的极坐标方程是
的极坐标方程是![]() ,即
,即![]() ,
,
化为普通方程得![]() ,即
,即![]() ,即
,即![]() .
.
因此,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)点![]() ,所以
,所以![]() 的直线方程为
的直线方程为![]() .
.
点![]() 为
为![]() 上任意一点,设点
上任意一点,设点![]() 的坐标为
的坐标为![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离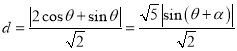 ,其中
,其中![]() 由
由![]() ,
,![]() 来确定.
来确定.
当![]() 时,
时,![]() ,
,
所以![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
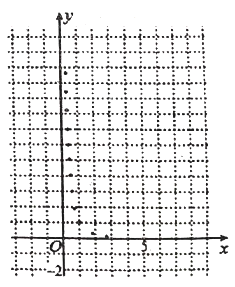
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为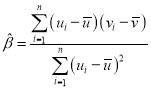 ,
,![]()