题目内容
设P=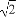 ,Q=
,Q= -
-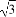 ,R=
,R=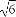 -
-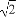 ,则P,Q,R的大小顺序是 .
,则P,Q,R的大小顺序是 .
P>R>Q
【解析】∵P=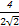 ,Q=
,Q=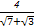 ,R=
,R=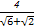 ,
,
而2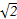 <
<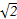 +
+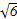 <
<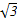 +
+ ,
,
∴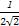 >
>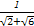 >
>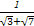 ,
,
故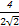 >
>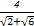 >
>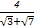 ,
,
即P>R>Q.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
题目内容
设P=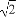 ,Q=
,Q= -
-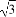 ,R=
,R=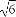 -
-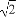 ,则P,Q,R的大小顺序是 .
,则P,Q,R的大小顺序是 .
P>R>Q
【解析】∵P=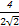 ,Q=
,Q=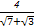 ,R=
,R=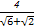 ,
,
而2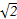 <
<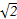 +
+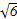 <
<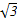 +
+ ,
,
∴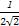 >
>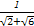 >
>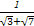 ,
,
故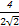 >
>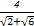 >
>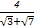 ,
,
即P>R>Q.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案