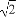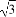题目内容
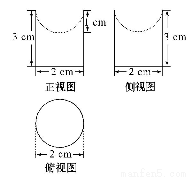
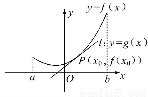
函数y=f′(x)是函数y=f(x)的导函数,且函数y=f(x)在点P(x0,f(x0))处的切线为l:y=g(x)=f′(x0)·(x-x0)+f(x0),F(x)=f(x)-g(x), 如果函数y=f(x)在区间[a,b]上的图象如图所示,且a<x0<b,那么( )
(A)F'(x0)=0,x=x0是F(x)的极大值点
(B)F'(x0)=0,x=x0是F(x)的极小值点
(C)F'(x0)≠0,x=x0不是F(x)的极值点
(D)F'(x0)≠0,x=x0是F(x)的极值点
B
【解析】【思路点拨】y=g(x)是函数y=f(x)在点P(x0,f(x0))处的切线,故g'(x)= f'(x0),据此判断F'(x0)是否为0,再进一步判断在x=x0两侧F'(x)的符号.
解:F'(x)=f'(x)-g'(x)=f'(x)-f'(x0),
∴F'(x0)=f'(x0)-f'(x0)=0,又当x<x0时,从图象上看,f'(x)<f'(x0),即F'(x)<0,此时函数F(x)=f(x)-g(x)为减函数,同理,当x>x0时,函数F(x)为增函数.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目