题目内容
1.已知函数f(x)=x2+2ax+2,求f(x)在[-5,5]上的最大值f(x)max=$\left\{\begin{array}{l}{27+10a,a>0}\\{27-10a,a≤0}\end{array}\right.$.分析 由于二次函数的对称轴为x=-a,分①当-a<-5、②当-5≤-a<0、③当0≤-a≤5、④当-a>5四种情况,分别利用二次函数的性质求得函数的最值
解答 解:∵函数f(x)=x2+2ax+2=(x+a)2+2-a2 的对称轴为x=-a,
①当-a<-5,即a>5时,函数y在[-5,5]上是增函数,
当x=5时,函数y取得最大值为27+10a.
②当-5≤-a<0,即0<a≤5时,当x=5时,函数y取得最大值为27+10a.
③当0≤-a≤5,即-5≤a≤0时,x=-a时,当x=-5时,函数y取得最大值为27-10a.
④当-a>5,即a<-5时,函数y在[-5,5]上是减函数,故当x=-5时,函数y取得最大值为27-10a;
∴f(x)max=$\left\{\begin{array}{l}{27+10a,a>0}\\{27-10a,a≤0}\end{array}\right.$,
故答案为:f(x)max=$\left\{\begin{array}{l}{27+10a,a>0}\\{27-10a,a≤0}\end{array}\right.$.
点评 本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
6.已知M是△ABC内一点,且$\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3},∠BAC={30°}$,若△MBC,△MCA,△MAB的面积分别为$\frac{1}{2},x,y$,则xy的最大值是( )
| A. | $\frac{1}{14}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{20}$ |
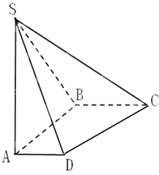 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,AD∥BC,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$ 四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列
四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列