题目内容
设函数f(x)=ax2+bx+c(a,b,c∈R).若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是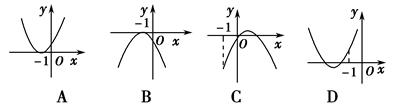
D
解析试题分析:由y=f(x)ex=ex(ax2+bx+c)⇒y'=f'(x)ex+exf(x)=ex[ax2+(b+2a)x+b+c],
由x=-1为函数f(x)ex的一个极值点可得,-1是方程ax2+(b+2a)x+b+c=0的一个根,
所以有a-(b+2a)+b+c=0⇒c=a.
法一:所以函数f(x)=ax2+bx+a,对称轴为x=- ,且f(-1)=2a-b,f(0)=a.
,且f(-1)=2a-b,f(0)=a.
对于A,由图得a>0,f(0)>0,f(-1)=0符合要求,
对于B,由图得a<0,f(0)<0,f(-1)=0不矛盾,
对于C,由图得a<0,f(0)<0,x=- >0得到b>0,f(-1)<0不矛盾,
>0得到b>0,f(-1)<0不矛盾,
对于D,由图得a>0,f(0)>0,x=- <-1得到b>2a,f(-1)<0于图中f(-1)>0矛盾,D不对.
<-1得到b>2a,f(-1)<0于图中f(-1)>0矛盾,D不对.
法二:得到函数f(x)=ax2+bx+a,由此得函数相应方程的两根之积为1,对照四个选项发现,D不成立,故选 D.
考点:本题主要考查应用导数研究函数的极值,二次函数图象和性质。
点评:易错题,本题要求“不可能”为的图象。研究函数的单调性、极值是导数的基本应用,方法明确,步骤规范。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
下列函数中既是奇函数,又在区间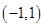 上是增函数的为( )
上是增函数的为( )
A.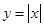 | B.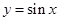 | C.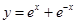 | D.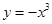 |
函数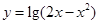 的单调递增区间为( )
的单调递增区间为( )
A.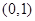 | B.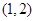 | C.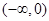 | D.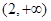 |
若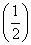 2a+1<
2a+1<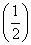 3-2a,则实数a的取值范围是( ).
3-2a,则实数a的取值范围是( ).
| A.(1,+∞) | B.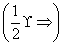 |
| C.(-∞,1) | D.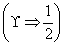 |
设函数 的图象上的点
的图象上的点 处的切线的斜率为
处的切线的斜率为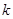 ,记
,记 ,则函数
,则函数 的图象大致为( )
的图象大致为( )
| A. | B. | C. | D. |
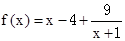 ,
,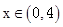 ,当
,当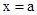 时,
时,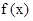 取得最小值
取得最小值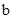 ,则函数
,则函数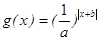 的图象为( )
的图象为( )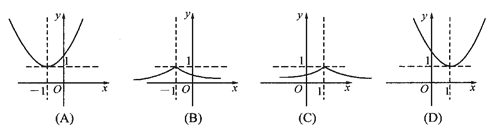
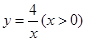 上,
上,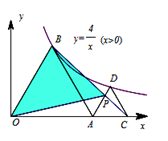
 B.
B. C.
C.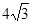 D.
D.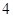

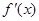 是函数
是函数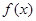 的导函数,将
的导函数,将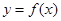 和
和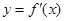 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )