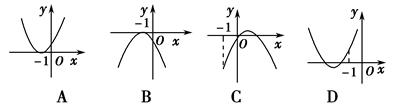
题目内容
设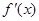 是函数
是函数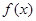 的导函数,将
的导函数,将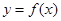 和
和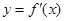 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )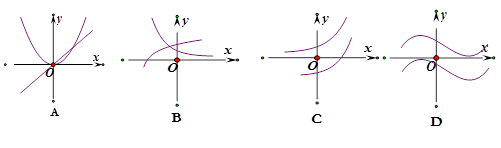
D
解析试题分析:本题可以考虑排除法,容易看出选项D不正确,因为D的图象,在整个定义域内,不具有单调性,但y=f(x)和y=f′(x)在整个定义域内具有完全相同的走势,不具有这样的函数. 解析:检验易知A、B、C均适合,不存在选项D的图象所对应的函数,在整个定义域内,不具有单调性,但y=f(x)和y=f′(x)在整个定义域内具有完全相同的走势,不具有这样的函数,故选D.
考点:函数单调性
点评:考查了函数单调性问题,以及函数的图像的特殊值排除法思想的应用,属于基础题。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
下列函数中,值域为 的是
的是
A. | B. | C. | D. |
函数 在[0,3]上的最大值、最小值分别是( )
在[0,3]上的最大值、最小值分别是( )
| A.-4,-15 | B.5,-4 | C.5,-15 | D.5,-16 |
下列函数中,在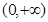 上为增函数的是 ( )
上为增函数的是 ( )
A.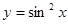 | B. |
C.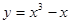 | D.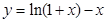 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B. | C. | D. |
函数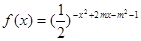 的单调增区间与值域相同,则实数
的单调增区间与值域相同,则实数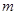 的取
的取
值为( )
A.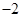 | B.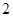 | C.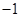 | D.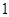 |
对于函数 与
与 ,若区间
,若区间 上
上 的最大值称为
的最大值称为 与
与 的“绝对差”,则
的“绝对差”,则 在
在 上的“绝对差”为
上的“绝对差”为
A. | B. | C. | D. |
 上的函数
上的函数 是减函数,且函数
是减函数,且函数 ,
, 满足不等式
满足不等式 .则当
.则当 时,
时, 的取值范围是( )
的取值范围是( )


