题目内容
14.古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1,3,6,10,第n个三角形数为$\frac{n(n+1)}{2}$=$\frac{1}{2}$n2+$\frac{1}{2}$n.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:三角形数 N(n,3)=$\frac{1}{2}$n2+$\frac{1}{2}$n
四边形数 N(n,4)=n2
五边形数 N(n,5)=$\frac{3}{2}$n2-$\frac{1}{2}$n
六边形数 N(n,6)=2n2-n
…
可以推测N(n,k)的表达式,由此计算N(20,15)的值为2490.
分析 观察已知式子的规律,并改写形式,归纳可得N(n,k)=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$n,把n=20,k=15代入可得答案.
解答 解:原已知式子可化为:N(n,3)=$\frac{1}{2}$n2+$\frac{1}{2}$n=$\frac{3-2}{2}{n}^{2}+\frac{4-3}{2}n$,
N(n,4)=n2=$\frac{4-2}{2}{n}^{2}+\frac{4-4}{2}n$,
N(n,5)=$\frac{3}{2}$n2-$\frac{1}{2}$n=$\frac{5-2}{2}{n}^{2}+\frac{4-5}{2}n$,
N(n,6)=2n2-n=$\frac{6-2}{2}{n}^{2}+\frac{4-6}{2}n$,
由归纳推理可得N(n,k)=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$n,
故N(20,15)=$\frac{15-2}{2}×{20}^{2}+\frac{4-15}{2}×20$=2490,
故答案为:2490
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知函数f(x)=-$\frac{1}{3}{x^3}+{x^2}$+ax-4在x=3处取得极值,则当f(sinα)+f′(cosβ),α,β∈[0,2π)取得最大值时,α+β=( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3π}{2}$ |
2.已知随机变量X服从正态分布,其正态分布密度曲线为函数f(x)=$\frac{1}{\sqrt{2π}}$e${\;}^{\frac{-(x-2)^{2}}{2}}$的图象,若${∫}_{0}^{2}$f(x)dx=$\frac{1}{3}$,则P(X>4)=( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
3.若f(tanx)=sin2x,则f(-1)的值是( )
| A. | 1 | B. | -1 | C. | 0.5 | D. | 0 |
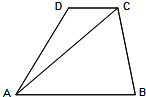 在梯形ABCD中,AB∥CD,CD=2,∠ADC=120°,cos$∠CAD=\frac{5\sqrt{7}}{14}$
在梯形ABCD中,AB∥CD,CD=2,∠ADC=120°,cos$∠CAD=\frac{5\sqrt{7}}{14}$