题目内容
6.已知命题p:?a∈[1,2],m2-10m+19≤$\sqrt{{a}^{2}+8}$;命题q:函数f(x)=3x2+2mx+m+6有两个零点.求使“p∧¬q”为真命题是实数m的取值范围.分析 分别解出关于命题p,q的m的范围,根据“p∧¬q”为真命题,得到不等式组,解出即可.
解答 解:对于命题p::?a∈[1,2],m2-10m+19≤$\sqrt{{a}^{2}+8}$;
∴m2-10m+19≤3,解得:2≤m≤8;
命题q:函数f(x)=3x2+2mx+m+6有两个零点,
∴△=4m2-12(m+6)>0,即:m2-3m-18>0,
解得:m>6或m<-3,
要使“p∧¬q”为真命题,
只需$\left\{\begin{array}{l}{2≤m≤8}\\{-3≤m≤6}\end{array}\right.$,
解得:2≤m≤6.
点评 本题考查了复合命题的判断,考查二次函数的性质以及函数恒成立问题,是一道基础题.

练习册系列答案
相关题目
16.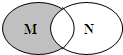 已知集合M={1,2,3},N={3,4,5},则图中阴影部分表示的集合是( )
已知集合M={1,2,3},N={3,4,5},则图中阴影部分表示的集合是( )
 已知集合M={1,2,3},N={3,4,5},则图中阴影部分表示的集合是( )
已知集合M={1,2,3},N={3,4,5},则图中阴影部分表示的集合是( )| A. | {3} | B. | {5} | C. | {1,2} | D. | {4,5} |
1.设a∈R,则“a>1”是“$\frac{1-{a}^{2}}{a}$<1-a”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.若a>b>0,则下列不等式成立的是( )
| A. | $\frac{1}{a}$+$\frac{1}{b}$>2$\sqrt{\frac{1}{ab}}$ | B. | ${a^{{-_{\;}}\frac{1}{2}}}>{b^{{-_{\;}}\frac{1}{2}}}$ | C. | ln(a-b)>0 | D. | 0.3a>0.3b |