题目内容
【题目】已知过原点![]() 的两条互相垂直的直线与抛物线
的两条互相垂直的直线与抛物线![]() 相交于不同于原点的两点
相交于不同于原点的两点![]() ,且
,且![]() 轴,
轴,![]() 的面积为16.
的面积为16.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
,![]() ,
,![]() 为抛物线
为抛物线![]() 上不同的三点,若
上不同的三点,若![]() ,试问:直线
,试问:直线![]() 是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
【答案】(1)![]() (2)过定点
(2)过定点![]()
【解析】
(1)不妨设点![]() 在第一象限,由
在第一象限,由![]() 轴知直线
轴知直线![]() ,
,![]() 的方程分别为
的方程分别为![]() ,
,![]() .代入抛物线方程得
.代入抛物线方程得![]() 的坐标,由
的坐标,由![]() 解得
解得![]() 值,得到答案;(2) 由(1)可得点
值,得到答案;(2) 由(1)可得点![]() . 设直线
. 设直线![]() 的方程并与抛物线联立,求出E,F的坐标,根据坐标写直线EF的方程,化简整理即可得到过的定点.
的方程并与抛物线联立,求出E,F的坐标,根据坐标写直线EF的方程,化简整理即可得到过的定点.
(1)不妨设点![]() 在第一象限,由题意知,直线
在第一象限,由题意知,直线![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,
,
则直线![]() ,
,![]() 的方程分别为
的方程分别为![]() ,
,![]() .
.
代入抛物线方程得![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
∴![]() .解得
.解得![]() .
.
故抛物线![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)可得点![]() .由题意可设直线
.由题意可设直线![]() 的方程为
的方程为![]() .
.
联立![]() 得
得![]() .
.
则![]() .∴
.∴![]() ,
,![]() .
.
同理可得![]() ,
,![]() .
.
∴直线![]() 的方程为
的方程为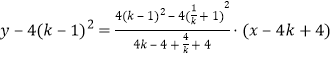 ,
,
即![]() .
.
∴![]()
![]()
![]()
![]() .
.
故直线![]() 过定点
过定点![]() .
.

【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能够有多大把握认为疫苗有效?
(参考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)在上述样本中从分数不少于120分的学生中,按照分层抽样的方法,抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名,若在这5名学生中随机抽取2人,求至少1人每周线上学习时间不足5小时的概率.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式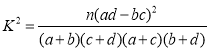 其中
其中![]() )
)
【题目】3月3日,武汉大学人民医院的团队在预印本平台![]() 上发布了一项研究:在新冠肺炎病例的统计数据中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例数据,发现
上发布了一项研究:在新冠肺炎病例的统计数据中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例数据,发现![]() 的患者为男性;进入重症监护病房的患者中,则有
的患者为男性;进入重症监护病房的患者中,则有![]() 为男性.随后,他们分析了武汉大学人民医院的数据.他们按照症状程度的不同进行分析,结果发现,男性患者有
为男性.随后,他们分析了武汉大学人民医院的数据.他们按照症状程度的不同进行分析,结果发现,男性患者有![]() 为危重,而女性患者危重情况的为
为危重,而女性患者危重情况的为![]() .也就是说男性的发病情况似乎普遍更严重.研究者总结道:“男性在新冠肺炎的传播中扮演着重要的角色.”那么,病毒真的偏爱男性吗?有一个中学生学习小组,在自己封闭的社区进行无接触抽样问卷调查,收集到男、女患者各50个数据,统计如下:
.也就是说男性的发病情况似乎普遍更严重.研究者总结道:“男性在新冠肺炎的传播中扮演着重要的角色.”那么,病毒真的偏爱男性吗?有一个中学生学习小组,在自己封闭的社区进行无接触抽样问卷调查,收集到男、女患者各50个数据,统计如下:
轻—中度感染 | 重度(包括危重) | 总计 | |
男性患者 |
|
|
|
女性患者 |
|
|
|
总计 |
|
|
|
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)能否有![]() 把握认为,新冠肺炎的感染程度和性别有关?
把握认为,新冠肺炎的感染程度和性别有关?
(3)该学生实验小组打算从“轻—中度感染”的患者中按男女比例再抽取5人,追踪某种中药制剂的效果.然后从这5人中随机抽取3人进行每日的健康记录,求至少抽到2名女性患者的概率.
附表及公式:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】自由购是通过自助结算方式购物的一种形式.某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取1名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
