题目内容
9.定义在R上的函数f(x)满足f′(x)>1-f(x),其中f′(x)是f(x)的导函数,e为自然对数的底数,则下列正确的是( )| A. | ef(1)-e>e2f(2)-e2 | |
| B. | e2015f(2015)-e2015>e2016f(2016)-e2016 | |
| C. | e2f(2)+e2>ef(1)+e | |
| D. | e2016f(2016)+e2016<e2015f(2015)+e2015 |
分析 根据选项中的不等式的形式可以想到构造一函数:设g(x)=exf(x)-ex,求导数,根据条件可以判断g′(x)>0,从而得出g(x)在R上单调递增,从而便可判断A,B错误;而同理构造函数:h(x)=exf(x)+ex,通过求导数,便可判断出h(x)在R上单调递增,这样便可判断选项C,D的正误,从而找出正确答案.
解答 解:设g(x)=exf(x)-ex,g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1];
∵f′(x)>1-f(x);
∴f(x)+f′(x)-1>0;
∴g′(x)>0;
∴g(x)在R上是增函数;
∴g(1)<g(2),即ef(1)-e<e2f(2)-e2,∴A错误;
g(2015)<g(2016),∴B错误;
同理,设h(x)=exf(x)+ex,由g′(x)>0得,h′(x)=exf(x)+exf′(x)+ex>0;
∴h(x)在R上单调递增;
∴h(2)>h(1),h(2016)>h(2015),∴C正确.
故选:C.
点评 考查通过构造函数解决问题的方法,根据导数符号判断函数单调性的方法,以及增函数定义的运用,通过观察选项中不等式的形式,从而构造函数是本题的关键,并要正确求导.

练习册系列答案
相关题目
18.若圆x2+y2-2x-4y=0的圆心到过原点的直线l的距离为1,则直线l的方程为( )
| A. | 3x-4y=0或x=0 | B. | 4x-3y=0 | ||
| C. | 3x-4y=0或4x-3y=0 | D. | 3x-4y=0 |
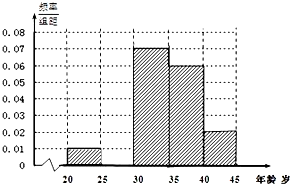 2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿,某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组:[20,25),[25,30),[30,35),[35,40),[40,45),根据调查结果得出年龄情况残缺的频率分布直方图如图所示.
2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿,某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组:[20,25),[25,30),[30,35),[35,40),[40,45),根据调查结果得出年龄情况残缺的频率分布直方图如图所示.