题目内容
12.在数列{an}中a1=1,an+1=an+$\frac{2}{{n}^{2}+2n}$,求an的通项公式.分析 由an+1=an+$\frac{2}{{n}^{2}+2n}$,得an+1-an=$\frac{1}{n}-\frac{1}{n+2}$,然后利用累加法求数列的通项公式.
解答 解:由an+1=an+$\frac{2}{{n}^{2}+2n}$,得an+1-an=$\frac{2}{{n}^{2}+2n}$=$\frac{2}{n(n+2)}=\frac{1}{n}-\frac{1}{n+2}$,
∴${a}_{2}-{a}_{1}=1-\frac{1}{3}$,
${a}_{3}-{a}_{2}=\frac{1}{2}-\frac{1}{4}$,
${a}_{4}-{a}_{3}=\frac{1}{3}-\frac{1}{5}$,
…
${a}_{n-1}-{a}_{n-2}=\frac{1}{n-2}-\frac{1}{n}$,
${a}_{n}-{a}_{n-1}=\frac{1}{n-1}-\frac{1}{n+1}$.
累加得:${a}_{n}-{a}_{1}=1+\frac{1}{2}-\frac{1}{n}-\frac{1}{n+1}=\frac{(n-1)(3n+2)}{2n(n+1)}$.
∴${a}_{n}=\frac{5{n}^{2}+n-2}{2{n}^{2}+2n}$.
点评 本题考查数列递推式,考查了累加法求数列的通项公式,是中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 20 | 80 |
| 北方学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2>k0) | 0.10 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
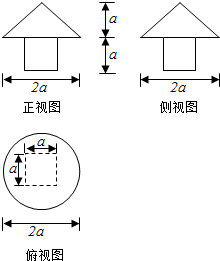 一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.
一个几何体的三视图如图,则它的表面积为4a2+(1+$\sqrt{2}$)πa2,体积为a3+$\frac{1}{3}{πa}^{3}$.