题目内容
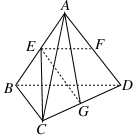
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
(1)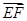 ·
·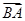 ;
;
(2)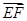 ·
·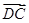 ;
;
(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.

(1)
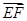 ·
·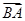 ;
;(2)
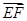 ·
·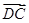 ;
;(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.
(1)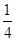 (2)-
(2)-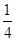 (3)
(3)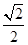 (4)
(4)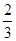
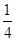 (2)-
(2)-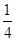 (3)
(3)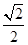 (4)
(4)
解:设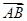 =a,
=a,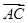 =b,
=b,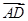 =c.
=c.
则|a|=|b|=|c|=1,
〈a,b〉=〈b,c〉=〈c,a〉=60°.
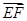 =
= BD=
BD= c-
c- a,
a,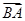 =-a,
=-a,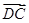 =b-c,
=b-c,
(1)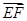 ·
·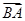 =(
=( c-
c- a)·(-a)
a)·(-a)
= a2-
a2- a·c=
a·c=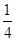 ;
;
(2)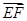 ·
·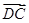 =
= (c-a)·(b-c)
(c-a)·(b-c)
= (b·c-a·b-c2+a·c)=-
(b·c-a·b-c2+a·c)=-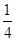 ;
;
(3)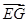 =
=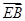 +
+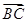 +
+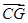
= a+b-a+
a+b-a+ c-
c- b=-
b=- a+
a+ b+
b+ c.
c.
|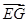 |2=
|2=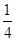 a2+
a2+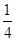 b2+
b2+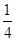 c2-
c2- a·b+
a·b+ b·c-
b·c- c·a=
c·a= .
.
即|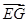 |=
|=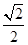 ,
,
所以EG的长为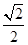 .
.
(4)设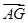 、
、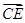 的夹角为θ.
的夹角为θ.
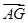 =
= b+
b+ c,
c,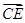 =
=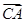 +
+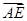 =-b+
=-b+ a,
a,
cosθ=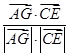 =-
=-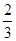 ,
,
由于异面直线所成角的范围是(0°,90°],
所以异面直线AG与CE所成角的余弦值为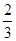 .
.
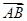 =a,
=a,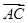 =b,
=b,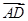 =c.
=c.则|a|=|b|=|c|=1,
〈a,b〉=〈b,c〉=〈c,a〉=60°.
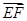 =
= BD=
BD= c-
c- a,
a,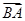 =-a,
=-a,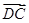 =b-c,
=b-c,(1)
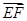 ·
·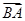 =(
=( c-
c- a)·(-a)
a)·(-a)=
 a2-
a2- a·c=
a·c=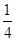 ;
;(2)
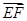 ·
·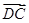 =
= (c-a)·(b-c)
(c-a)·(b-c)=
 (b·c-a·b-c2+a·c)=-
(b·c-a·b-c2+a·c)=-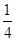 ;
;(3)
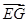 =
=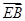 +
+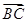 +
+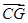
=
 a+b-a+
a+b-a+ c-
c- b=-
b=- a+
a+ b+
b+ c.
c.|
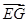 |2=
|2=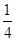 a2+
a2+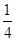 b2+
b2+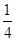 c2-
c2- a·b+
a·b+ b·c-
b·c- c·a=
c·a= .
.即|
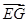 |=
|=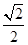 ,
,所以EG的长为
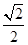 .
.(4)设
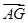 、
、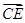 的夹角为θ.
的夹角为θ.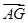 =
= b+
b+ c,
c,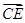 =
=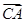 +
+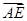 =-b+
=-b+ a,
a,cosθ=
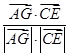 =-
=-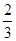 ,
,由于异面直线所成角的范围是(0°,90°],
所以异面直线AG与CE所成角的余弦值为
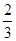 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
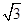 ,E是PB上任意一点.
,E是PB上任意一点.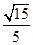 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.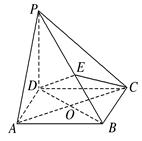
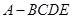 中,平面
中,平面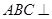 平面
平面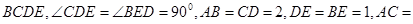
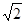 .
.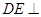 平面
平面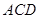 ;
;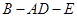 的大小
的大小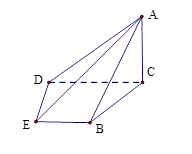
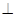 平面AEB,AE
平面AEB,AE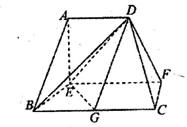
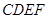 为正方形,面
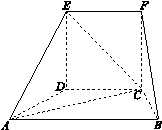
为正方形,面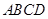 为等腰梯形,
为等腰梯形,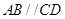 ,
,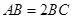 ,
,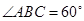 ,且平面
,且平面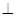 平面
平面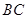 与平面
与平面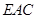 所成角的正弦值;
所成角的正弦值;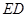 上是否存在点
上是否存在点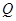 ,使平面
,使平面 ?
?
 ,
,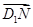 〉的值为( )
〉的值为( )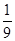
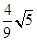
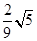

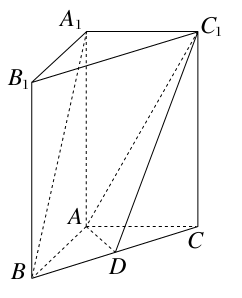
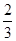 A1D,AF=
A1D,AF=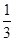 AC,则( )
AC,则( )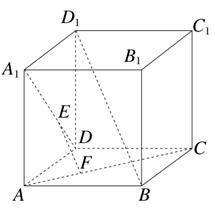
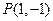 到直线
到直线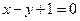 的距离是________________.
的距离是________________.