题目内容
13.已知定义在R上的函数f(x)的图象是连续不断的一条曲线,若存在实数t,使得f(x+t)+tf(x)=0对任意x都成立,则称f(x)是“回旋函数”.给下列四个命题:①函数f(x)=x+1不是“回旋函数”;
②函数f(x)=x2是“回旋函数”;
③若函数f(x)=ax(a>1)是“回旋函数”,则t<0;
④若函数f(x)是t=2时的“回旋函数”,则f(x)在[0,4030]上至少有2015个零点.
其中为真命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①利用回旋函数的定义即可.
②利用回旋函数的定义,令x=0,则必须有a=0;令x=1,则有a2+3a+1=0,故可判断;
③若指数函数y=ax为阶数为t回旋函数,根据定义求解,得出结论.
④由定义得到f(x+2)=-2f(x),由零点存在定理得,在区间(x,x+2)上必有一个零点令x=0,2,2×2,3×2,…,2015×2,即可得到
解答 解:对于①函数f(x)=x+1为回旋函数,则由f(x+t)+tf(x)=0,得x+t+1+t(x+1)=0,t(x+2)=-1-x,∴t=-$\frac{x+1}{x+2}$,故结论正确.
对于.②函数f(x)=x2是“回旋函数”若(x+t)2+tx2=0对任意实数都成立,令x=0,则必须有t=0,令x=1,则有t2+3t+1=0,显然t=0不是这个方程的解,故假设不成立,该函数不是回旋函数,故结论不正确;
对于③,若指数函数y=ax为阶数为t回旋函数,则ax+t+tax=0,at+t=0,∴t<0,∴结论成立,
对于④:若f(x)是t=2的回旋函数,则f(x+2)+2f(x)=0对任意的实数x都成立,即有f(x+2)=-2f(x),则f(x+2)与f(x)异号,由零点存在定理得,在区间(x,x+2)上必有一个零点,可令x=0,2,4,6,…,2015×2,则函数f(x)在[0,4030]上至少存在2015个零点.故结论正确
故真命题为:①③④,
故选:C.
点评 本题考查新定义的理解和运用,考查函数的周期、函数的零点注意转化为函数的图象的交点个数,考查数形结合的能力,以及运算能力,属于中档题

练习册系列答案
相关题目
2.若x、y∈R,则不等式xy(x-y)>0成立的一个充要条件是( )
| A. | x<0<y | B. | y<x<0 | C. | $\frac{1}{x}$<$\frac{1}{y}$ | D. | x>y>0 |
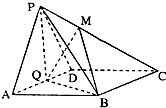 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.