题目内容
3.双曲线C:$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1的离心率为$\frac{\sqrt{6}}{2}$;渐近线的方程为y=±$\frac{\sqrt{2}}{2}$x.分析 由双曲线方程求出三参数a,b,c,再根据离心率公式求出离心率,渐近线的方程公式求出渐近线的方程.
解答 解:∵双曲线的方程是$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1,
∴a2=8,b2=4,
∴c2=a2+b2=12,
∴a=2$\sqrt{2}$,b=2,c=2$\sqrt{3}$,
∴离心率为e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$,渐近线的方程为y=±$\frac{\sqrt{2}}{2}$x,
故答案为:$\frac{\sqrt{6}}{2}$,y=±$\frac{\sqrt{2}}{2}$x.
点评 本题的考点是双曲线的简单性质,考查由双曲线的方程求三参数,考查双曲线中三参数的关系:c2=a2+b2

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

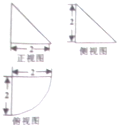 某几何体的三视图如图所示,其中正视图和侧视图均为等腰直角三角形,俯视图是圆心角为直角的扇形,则该几何体的体积为$\frac{2π}{3}$.
某几何体的三视图如图所示,其中正视图和侧视图均为等腰直角三角形,俯视图是圆心角为直角的扇形,则该几何体的体积为$\frac{2π}{3}$.