题目内容
用列举法表示集合:
(1)A={x∈N|
∈N}= ;
(2)B={
∈N|x∈N}= .
(1)A={x∈N|
| 6 |
| 6-x |
(2)B={
| 6 |
| 6-x |
考点:集合的表示法
专题:集合
分析:(1)首先,6-x是6的约数,给x的取值,x的取值0,1,2,3,4,5,然后进行验证即可;
(2)给x一些取值0,1,2,3,4,5,然后进行验证.
(2)给x一些取值0,1,2,3,4,5,然后进行验证.
解答:解:(1)当x=0时,
=1∈N,
当x=1时,
=
∉N,
当x=2时,
=
∉N,
当x=3时,
=2∈N,
当x=4时,
=3∈N,
当x=5时,
=6∈N,
∴A={0,3,4,5}.
(2)当x=0时,
=1∈N,此时x=0符合条件;
当x=1时,
=
∉N,此时x=1不符合条件;
当x=2时,
=
∉N,此时x=2不符合条件;
当x=3时,
=2∈N,此时x=3符合条件;
当x=4时,
=3∈N,此时x=4符合条件;
当x=5时,
=6∈N,此时x=5符合条件.
∴B={1,2,3,6}.
故答案为:(1){0,3,4,5};(2){1,2,3,6}.
| 6 |
| 6-0 |
当x=1时,
| 6 |
| 6-1 |
| 6 |
| 5 |
当x=2时,
| 6 |
| 6-2 |
| 3 |
| 2 |
当x=3时,
| 6 |
| 6-3 |
当x=4时,
| 6 |
| 6-4 |
当x=5时,
| 6 |
| 6-5 |
∴A={0,3,4,5}.
(2)当x=0时,
| 6 |
| 6-0 |
当x=1时,
| 6 |
| 6-1 |
| 6 |
| 5 |
当x=2时,
| 6 |
| 6-2 |
| 3 |
| 2 |
当x=3时,
| 6 |
| 6-3 |
当x=4时,
| 6 |
| 6-4 |
当x=5时,
| 6 |
| 6-5 |
∴B={1,2,3,6}.
故答案为:(1){0,3,4,5};(2){1,2,3,6}.
点评:本题主要考查集合的列举法,掌握常见数集的表示方法,理解描述法和列举法的区别,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知不等式{x|ax-2>0}的解集为{x|x<-4},则a的值为( )
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
设全集为R,集合A={x|x<1},B={x|
>0},则( )
| 1 |
| x-2 |
| A、(∁RA)⊆B |
| B、A⊆(∁RB) |
| C、A⊆B |
| D、B⊆A |
已知集合A={x|x2-2x≤0},B={x|x≥a},若A∪B=B,则实数a的取值范围时( )
| A、(-∞,0) | B、(-∞,0] | C、(0,+∞) | D、[0,+∞) |
 (
( )任意排成
)任意排成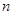 行
行 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若 表示某个
表示某个 行第
行第 列的数(
列的数( ,
, ),且满足
),且满足 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________