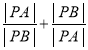题目内容
【题目】已知函数![]() .
.
(1)若![]() 是
是![]() 的一个极值点,判断
的一个极值点,判断![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.(2)见解析
单调递增.(2)见解析
【解析】
(1)求出导函数,由极值点求出参数![]() ,确定
,确定![]() 的正负得
的正负得![]() 的单调性;
的单调性;
(2)求出![]() ,得极值点
,得极值点![]() 满足:
满足: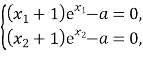
所以![]() ,由(1)即
,由(1)即![]() ,不妨设
,不妨设![]() .要证
.要证![]() ,则只要证
,则只要证![]() ,而
,而![]() ,因此由
,因此由![]() 的单调性,只要能证
的单调性,只要能证![]() ,即
,即![]() 即可.令
即可.令![]() ,利用导数的知识可证得结论成立.
,利用导数的知识可证得结论成立.
(1)由已知得![]() .
.
因为![]() 是
是![]() 的一个极值点,所以
的一个极值点,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
又当![]() 时,
时,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)![]() ,因此极值点
,因此极值点![]() 满足:
满足: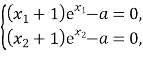
所以![]() 由(1)即
由(1)即![]() ,不妨设
,不妨设![]() .
.
要证![]() ,则只要证
,则只要证![]() ,而
,而![]() ,因此由
,因此由![]() 的单调性,只要能证
的单调性,只要能证![]() ,即
,即![]() 即可.
即可.
令![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() 在
在![]() 单调递增,又
单调递增,又![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: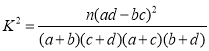 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |