题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且点
,且点![]()
![]() 在函数
在函数![]() 的图像上;
的图像上;
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)在第(2)问的条件下,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
【答案】(1)![]() (2)当n为偶数时,
(2)当n为偶数时,![]() ;当n为奇数时,
;当n为奇数时,![]() .(3)
.(3)![]()
【解析】
(1)根据![]() ,讨论
,讨论![]() 与
与![]() 两种情况,即可求得数列
两种情况,即可求得数列![]() 的通项公式;
的通项公式;
(2)由(1)利用递推公式及累加法,即可求得当n为奇数或偶数时![]() 的通项公式.也可利用数学归纳法,先猜想出通项公式,再用数学归纳法证明.
的通项公式.也可利用数学归纳法,先猜想出通项公式,再用数学归纳法证明.
(3)分类讨论,当n为奇数或偶数时,分别求得![]() 的最大值,即可求得
的最大值,即可求得![]() 的取值范围.
的取值范围.
(1)由题意可知,![]() .
.
当![]() 时,
时,![]()
![]()
![]() ,
,
当![]() 时,
时,![]()
![]() 也满足上式.
也满足上式.
所以![]() .
.
(2)解法一:由(1)可知![]()
![]() ,
,
即![]()
![]() .
.
当![]() 时,
时,![]() ,①
,①
当![]() 时,
时,![]() ,所以
,所以![]() ,②
,②
当![]() 时,
时,![]() ,③
,③
当![]() 时,
时,![]() ,所以
,所以![]() ,④
,④
……
当![]() 时,n为偶数
时,n为偶数![]()
当![]() 时,n为偶数所以
时,n为偶数所以![]()
以上![]() 个式子相加,得
个式子相加,得
![]()
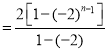
![]() .
.
又![]() ,所以当n为偶数时,
,所以当n为偶数时,![]() .
.
同理,当n为奇数时,
![]()
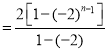
![]() ,
,
所以,当n为奇数时,![]() .
.
解法二:
猜测:当n为奇数时,
![]()

![]() .
.
猜测:当n为偶数时,
![]()

![]() .
.
以下用数学归纳法证明:
![]() ,命题成立;
,命题成立;
假设当![]() 时,命题成立;
时,命题成立;
当n为奇数时,![]() ,
,
当![]() 时,n为偶数,由
时,n为偶数,由![]()
![]() 得
得
![]()
故,![]() 时,命题也成立.
时,命题也成立.
综上可知, 当n为奇数时![]()
同理,当n为偶数时,命题仍成立.
(3)由(2)可知 .
.
①当n为偶数时,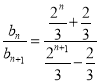
![]()
![]() ,
,
所以![]() 随n的增大而减小从而当n为偶数时,
随n的增大而减小从而当n为偶数时,![]() 的最大值是
的最大值是![]() .
.
②当n为奇数时,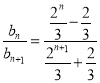
![]()
![]() ,
,
所以![]() 随n的增大而增大,且
随n的增大而增大,且![]() .
.
综上,![]() 的最大值是1.
的最大值是1.
因此,若对于任意的![]() ,不等式
,不等式![]() 恒成立,只需
恒成立,只需![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .
.

 优生乐园系列答案
优生乐园系列答案【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: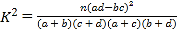 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |