题目内容
【题目】已知椭圆
的离心率为
，其左顶点
在圆
上.
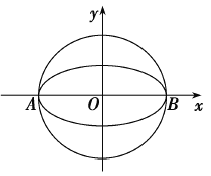
（1）求椭圆
的方程；
（2）若点
为椭圆上不同于点 的点，直线
与圆
的另一个交点为
.是否存在点，使得
?若存在，求出点的坐标；若不存在，说明理由.
【答案】(1) 
(2) 不存在直线
，使得
【解析】
（1）由题意求出a，通过离心率求出c，然后求解椭圆的标准方程；
（2）设点
，
，设直线的方程为
，与椭圆方程联立，利用弦长公式求出
，利用垂径定理求出
，从而整理即可得到结果.
（1）因为椭圆
的左顶点
在圆
上，令
，得
，所以
，
又离心率为
，所以
，所以
，
所以
，
所以的方程为.
（2）设点，，设直线的方程为，
与椭圆方程联立得
化简得到
，
因为
为方程的一个根，
所以
，所以
，
所以
.
因为圆心到直线的距离为
，
所以
，
因为
，
代入得到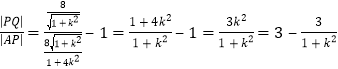
，
显然
，所以不存在直线，使得.
练习册系列答案
相关题目
【题目】某旅游风景区发行的纪念章即将投放市场，根据市场调研情况，预计每枚该纪念章的市场价y（单位：元）与上市时间x（单位：天）的数据如下：
上市时间x天 | 2 | 6 | 20 |
市场价y元 | 102 | 78 | 120 |
（1）根据上表数据，从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系并说明理由：①
；②
；③
；
（2）利用你选取的函数，求该纪念章市场价最低时的上市天数及最低的价格；
（3）利用你选取的函数，若存在
，使得不等式
成立，求实数k的取值范围.
【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（
个月）和市场占有率（
）的几组相关对应数据：
| 1 | 2 | 3 | 4 | 5 |
| 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
（1）根据上表中的数据，用最小二乘法求出
关于的线性回归方程；
（2）根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过
（精确到月）.
