题目内容
(本小题满分13分)
已知椭圆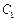 和抛物线
和抛物线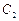 有公共焦点F(1,0),
有公共焦点F(1,0), 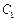 的中心和
的中心和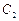 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线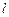 与抛物线
与抛物线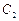 分别相交于A,B两点.
分别相交于A,B两点.
(Ⅰ)写出抛物线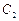 的标准方程;
的标准方程;
(Ⅱ)若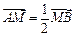 ,求直线
,求直线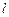 的方程;
的方程;
(Ⅲ)若坐标原点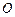 关于直线
关于直线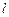 的对称点
的对称点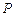 在抛物线
在抛物线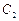 上,直线
上,直线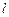 与椭圆
与椭圆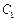 有公共点,求椭圆
有公共点,求椭圆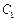 的长轴长的最小值.
的长轴长的最小值.
已知椭圆
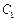 和抛物线
和抛物线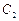 有公共焦点F(1,0),
有公共焦点F(1,0), 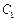 的中心和
的中心和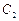 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线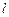 与抛物线
与抛物线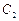 分别相交于A,B两点.
分别相交于A,B两点.(Ⅰ)写出抛物线
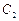 的标准方程;
的标准方程;(Ⅱ)若
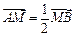 ,求直线
,求直线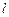 的方程;
的方程;(Ⅲ)若坐标原点
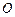 关于直线
关于直线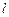 的对称点
的对称点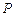 在抛物线
在抛物线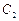 上,直线
上,直线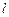 与椭圆
与椭圆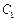 有公共点,求椭圆
有公共点,求椭圆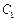 的长轴长的最小值.
的长轴长的最小值.(1) (2)
(2) 或
或 (3)
(3)
 (2)
(2) 或
或 (3)
(3)
(Ⅰ)由题意,抛物线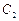 的方程为:
的方程为: , …………2分
, …………2分
(Ⅱ)设直线 的方程为:
的方程为: .
.

联立 ,消去
,消去 ,得
,得 , ……………3分
, ……………3分
显然 ,设
,设 ,
,
则 ①
①
 ② …………………4分
② …………………4分
又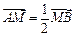 ,所以
,所以 ③ …………………5分
③ …………………5分
由①②③消去 ,得
,得  ,
,
故直线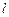 的方程为
的方程为 或
或 . …………………6分
. …………………6分
(Ⅲ)设 ,则
,则 中点为
中点为 ,因为
,因为 两点关于直线
两点关于直线 对称,
对称,
所以 ,即
,即 ,解之得
,解之得 , …………………8分
, …………………8分
将其代入抛物线方程,得:
 ,所以,
,所以, . ………………………9分
. ………………………9分
联立 ,消去
,消去 ,得:
,得:
 . ………………………10分
. ………………………10分
由 ,得
,得
 ,即
,即 , …………………12分
, …………………12分
将 ,
, 代入上式并化简,得
代入上式并化简,得
 ,所以
,所以 ,即
,即 ,
,
因此,椭圆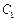 长轴长的最小值为
长轴长的最小值为 . ………………………13分
. ………………………13分
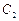 的方程为:
的方程为: , …………2分
, …………2分(Ⅱ)设直线
 的方程为:
的方程为: .
.
联立
 ,消去
,消去 ,得
,得 , ……………3分
, ……………3分显然
 ,设
,设 ,
,则
 ①
① ② …………………4分
② …………………4分又
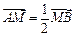 ,所以
,所以 ③ …………………5分
③ …………………5分由①②③消去
 ,得
,得  ,
, 故直线
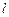 的方程为
的方程为 或
或 . …………………6分
. …………………6分(Ⅲ)设
 ,则
,则 中点为
中点为 ,因为
,因为 两点关于直线
两点关于直线 对称,
对称,所以
 ,即
,即 ,解之得
,解之得 , …………………8分
, …………………8分将其代入抛物线方程,得:
 ,所以,
,所以, . ………………………9分
. ………………………9分联立
 ,消去
,消去 ,得:
,得: . ………………………10分
. ………………………10分由
 ,得
,得 ,即
,即 , …………………12分
, …………………12分将
 ,
, 代入上式并化简,得
代入上式并化简,得 ,所以
,所以 ,即
,即 ,
, 因此,椭圆
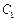 长轴长的最小值为
长轴长的最小值为 . ………………………13分
. ………………………13分
练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
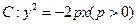 上横坐标为
上横坐标为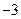 的一点与其焦点
的一点与其焦点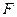 的距离为
的距离为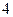 .
.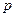 的值;
的值;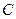 上各点向
上各点向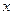 轴作垂线段,求垂线段中点的轨迹方程.
轴作垂线段,求垂线段中点的轨迹方程.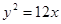 上的点
上的点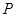 与焦点的距离为
与焦点的距离为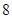 ,则
,则


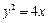 的焦点为F,
的焦点为F,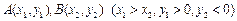 在抛物线上,且存在实数λ,使
在抛物线上,且存在实数λ,使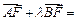 0,
0,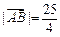 .
. ,0) B.(
,0) B.(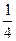 ,0) C.(0,
,0) C.(0,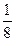 )
)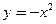 的焦点坐标为( )
的焦点坐标为( ) )
) )
)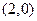 的距离和它到定直线
的距离和它到定直线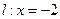 的距离相等,则点P的轨迹方程为_________.
的距离相等,则点P的轨迹方程为_________.