题目内容
20.设集合A={x|x2+2x-3<0},集合B={x||x+a|<1}.(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围.
分析 (1)通过解不等式,求出集合A、B,从而求出其并集即可;(2)问题转化为集合B是集合A的真子集,得到关于a的不等式组,解出即可.
解答 解:(1)解不等式x2+2x-3<0,
得-3<x<1,即A=(-3,1),…(2分)
当a=3时,由|x+3|<1,
解得-4<x<-2,即集合B=(-4,-2),…(4分)
所以A∪B=(-4,1);…(6分)
(2)因为p是q成立的必要不充分条件,
所以集合B是集合A的真子集…(8分)
又集合A=(-3,1),B=(-a-1,-a+1),…(10分)
所以$\left\{\begin{array}{l}-a-1≥-3\\-a+1<1\end{array}\right.$或$\left\{\begin{array}{l}-a-1>-3\\-a+1≤1\end{array}\right.$,…(12分)
解得0≤a≤2,
即实数a的取值范围是0≤a≤2…(14分)
点评 本题考查了解不等式问题,考查充分必要条件,考查集合的包含关系,是一道基础题.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
10.已知函数f(x)和g(x)分别是定义在[-10,10]上的奇函数和偶函数,则函数F(x)=f(x)•g(x)的图象关于( )
| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
5.已知M={x∈N|$\frac{6}{6-x}$∈N},则集合M的子集的个数是( )
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
9.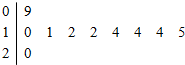 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
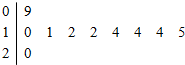 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )| A. | 12 | B. | 14 | C. | 15 | D. | 17 |
10.函数f(x)=$\sqrt{x+3}$+$\frac{1}{lg(x+1)}$的定义域是( )
| A. | (-1,0)∪(0,+∞) | B. | [-3,+∞) | C. | [-3,-1)∪(-1,+∞) | D. | (-1,+∞) |
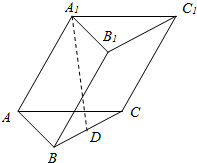 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.