题目内容
【题目】已知函数![]() 在
在![]() 处取得极值
处取得极值![]() ,其中
,其中![]() 为常数.若对任意
为常数.若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】![]() .
.
【解析】试题分析: 函数![]() 在
在![]() 处取得极值
处取得极值![]() ,即
,即![]() ,
, ![]() ,列出方程组可求出a,b的值,代入函数
,列出方程组可求出a,b的值,代入函数![]() 求出解析式,对函数求导判断单调性,求出函数的极小值, 且此极小值也是最小值, 要使
求出解析式,对函数求导判断单调性,求出函数的极小值, 且此极小值也是最小值, 要使![]() 对任意
对任意![]() 恒成立,只需
恒成立,只需![]() 小于等于函数的最小值,代入解出c的取值范围即可.
小于等于函数的最小值,代入解出c的取值范围即可.
试题解析:
由题意知f(1)=b-c=-3-c,因此b=-3.
对f(x)求导,得
f′(x)=4ax3ln x+ax4·![]() +4bx3
+4bx3
=x3(4aln x+a+4b).
由题意知f′(1)=0,得a+4b=0,解得a=12,
从而f′(x)=48x3ln x(x>0).令f′(x)=0,解得x=1.
当0<x<1时,f′(x)<0,此时f(x)为减函数;
当x>1时,f′(x)>0,此时f(x)为增函数.
所以f(x)在x=1处取得极小值f(1)=-3-c,
并且此极小值也是最小值.
所以要使f(x)≥-2c2(x>0)恒成立,只需-3-c≥-2c2即可.
整理得2c2-c-3≥0,解得c≥![]() 或c≤-1.
或c≤-1.
所以c的取值范围为![]() .
.
点睛: 本题考查利用导数判断函数的单调性,求函数的极值和最值以及函数的恒成立问题,属于中档题目.恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解,注意利用数形结合的数学思想方法.

 名校课堂系列答案
名校课堂系列答案【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
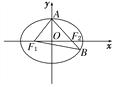
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.