题目内容
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
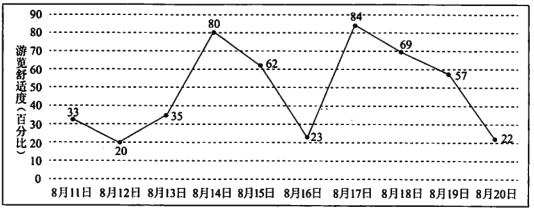
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
【答案】 (1)![]() ;(2)
;(2)![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
![]() 的期望
的期望![]() ;(3)从8月16日开始连续三天游览舒适度的方差最大.
;(3)从8月16日开始连续三天游览舒适度的方差最大.
【解析】试题分析:(1)本题考查古典概型概率问题,分析题意可知,小明到达公园并连续游览两天的事件总数为9个,若连续两天都遇上拥挤,由图可知,应为8月14日和8月15日,8月17日和8月18日,所以连续两天都遇上拥挤的概率为2/9;(2)本题考查离散型随机变量分布列,分析可知X的所以可能取值为0,1,2,X=2时为8月11日和8月12日,8月12日和8月13日,所以![]() ,X=0时为8月14日和8月15日,8月17日和8月18日,8月18日和8月19日,所以
,X=0时为8月14日和8月15日,8月17日和8月18日,8月18日和8月19日,所以![]() ,则
,则![]() ,于是可以求出分布列和数学期望;(3)由图分析,8月16日开始连续三天舒适度方差最大.
,于是可以求出分布列和数学期望;(3)由图分析,8月16日开始连续三天舒适度方差最大.
试题解析:设![]() 表示事件“小明8月11日起第
表示事件“小明8月11日起第![]() 日连续两天游览主題公园”
日连续两天游览主題公园” ![]() ,根据题意,
,根据题意, ![]() ,且
,且![]() .
.
(1)设![]() 为事件“小明连续两天都遇上拥挤”.则
为事件“小明连续两天都遇上拥挤”.则 ![]() ,所以
,所以
![]() .
.
(2)由题意,可知![]() 的所有可能取值为
的所有可能取值为![]() .且
.且![]() ;
;
![]() ;
;
![]() ,所以
,所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
故![]() 的期望
的期望![]() .
.
(3)从8月16日开始连续三天游览舒适度的方差最大.

练习册系列答案
相关题目


