Question

7．如图，给定双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，其右顶点为A，右焦点为F，l为其右准线．MN过焦点F的弦，射线NA、MA分别与准线l交于点C、D，P为线段CD的中点，证明：PF⊥MN．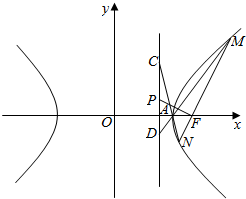

Answer 1

分析 设过点F（c，0）的直线l方程为：y=k（x-c），点M（x₁，y₁），N（x₂，y₂），将直线l方程y=k（x-c）代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，整理得：（b²-a²k²）x²-2ca²k²x+a²k²c²-a²b²=0，由此利用已知条件推导出直线PF₂的斜率为k′=-$\frac{1}{k}$，从而能够证明k•k′=-1，即可证明结论．

解答 证明：设过点F（c，0）的直线l方程为：y=k（x-c），
设点M（x₁，y₁），点N（x₂，y₂）
将直线l方程y=k（x-c）代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，
整理得：（b²-a²k²）x²-2ca²k²x+a²k²c²-a²b²=0，
∴x₁+x₂=$\frac{2c{a}^{2}{k}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$，x₁x₂=$\frac{{a}^{2}{k}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$①
直线AM的方程为：y=$\frac{{y}_{1}}{{x}_{1}-a}$（x-a），直线AN的方程为：y=$\frac{{y}_{2}}{{x}_{2}-a}$（x-a），
令x=$\frac{{a}^{2}}{c}$，得点M（$\frac{{a}^{2}}{c}$，$\frac{{y}_{1}}{{x}_{1}-a}$（$\frac{{a}^{2}}{c}$-a）），N（$\frac{{a}^{2}}{c}$，$\frac{{y}_{2}}{{x}_{2}-a}$（$\frac{{a}^{2}}{c}$-a）），
∴点P的坐标（$\frac{{a}^{2}}{c}$，$\frac{1}{2}$[$\frac{{y}_{1}}{{x}_{1}-a}$（$\frac{{a}^{2}}{c}$-a））+$\frac{{y}_{2}}{{x}_{2}-a}$（$\frac{{a}^{2}}{c}$-a）]，
直线PF的斜率为k′={$\frac{1}{2}$[$\frac{{y}_{1}}{{x}_{1}-a}$（$\frac{{a}^{2}}{c}$-a））+$\frac{{y}_{2}}{{x}_{2}-a}$（$\frac{{a}^{2}}{c}$-a）]}÷（$\frac{{a}^{2}}{c}$-c）
=$\frac{1}{2}$•$\frac{a}{a+c}$•（$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$）②
①②联立化简，可得直线PF的斜率为k′=-$\frac{1}{k}$
∴kk′=-1，
∴PF⊥MN．

点评 本小题考查直线与圆锥曲线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想等．