题目内容
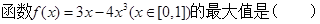
| A.1 | B.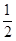 | C.0 | D.-1 |
A
析:先求导数,根据函数的单调性研究出函数的极值点,连续函数f(x)在区间(0,1)内只有一个极值,那么极大值就是最大值,从而求出所求.
解答:解:f’(x)=3-12x2=3(1-2x)(1+2x)
令f’(x)=0,解得:x=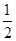 或-
或-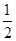 (舍去)
(舍去)
当x∈(0,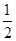 )时,f’(x)>0,当x∈(
)时,f’(x)>0,当x∈(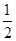 ,1)时,f’(x)<0,
,1)时,f’(x)<0,
∴当x=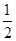 时f(x)(x∈[0,1])的最大值是f(
时f(x)(x∈[0,1])的最大值是f(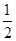 )=1
)=1
故选A.
点评:本题考查了利用导数求闭区间上函数的最值,连续函数在区间(a,b)内只有一个极值,那么极大值就是最大值,属于基础题.
解答:解:f’(x)=3-12x2=3(1-2x)(1+2x)
令f’(x)=0,解得:x=
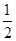 或-
或-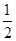 (舍去)
(舍去)当x∈(0,
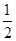 )时,f’(x)>0,当x∈(
)时,f’(x)>0,当x∈(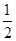 ,1)时,f’(x)<0,
,1)时,f’(x)<0,∴当x=
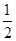 时f(x)(x∈[0,1])的最大值是f(
时f(x)(x∈[0,1])的最大值是f(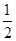 )=1
)=1故选A.
点评:本题考查了利用导数求闭区间上函数的最值,连续函数在区间(a,b)内只有一个极值,那么极大值就是最大值,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
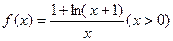
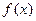 在区间
在区间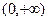
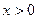 时,
时,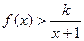 恒成立,求正整数
恒成立,求正整数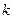 的最大值。
的最大值。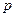 :函数
:函数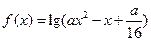 的定义域为
的定义域为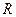 ;
;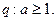 如果命题“
如果命题“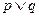 为真,
为真,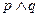 为假”,求实数
为假”,求实数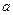 的取值范围.
的取值范围.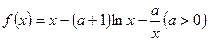 。
。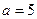 时,求函数
时,求函数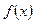 的单调递增区间;
的单调递增区间;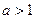 ,函数
,函数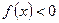 在
在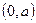 上恒成立。
上恒成立。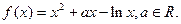
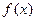 在
在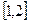 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;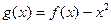 ,是否存在实数
,是否存在实数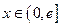 (
(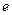 是自然常数)时,函数
是自然常数)时,函数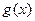
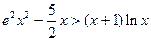 .
.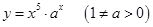 的导数是
的导数是 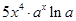
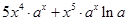
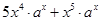
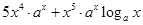
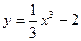 以点(1,-
以点(1,-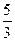 )为切点的切线的倾斜角为
)为切点的切线的倾斜角为 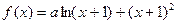 在
在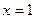 处有极值
处有极值 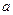 值;
值;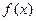 的单调区间
的单调区间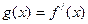 ,若曲线
,若曲线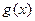 在
在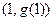 处的切线与两坐标轴分别交于
处的切线与两坐标轴分别交于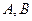 两点(
两点( 为坐标原点),求
为坐标原点),求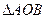 的面积
的面积