题目内容
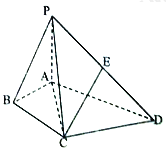
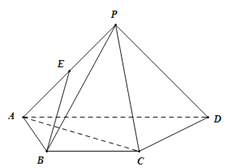
【题目】如图,四棱锥![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 和
和![]() 是两个边长为2的正三角形,
是两个边长为2的正三角形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
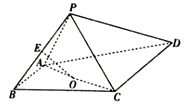
(1)证明:![]() 平面
平面![]() .
.
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(1)见解析;(2)当![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】
(1)设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,证明OE为三角形BPF的中位线,得
,证明OE为三角形BPF的中位线,得![]() 即可证明(2)证明
即可证明(2)证明![]() 平面
平面![]() ,由
,由![]() ,过
,过![]() 分别作
分别作![]() ,
,![]() 的平行线,分别以它们作为
的平行线,分别以它们作为![]() 轴,以
轴,以![]() 为
为![]() 轴建立如图所示的空间直角坐标系,求平面
轴建立如图所示的空间直角坐标系,求平面![]() 的法向量,假设线段
的法向量,假设线段![]() 上存在一点
上存在一点![]() ,设
,设![]() ,得
,得![]() ,由直线
,由直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 列
列![]() 的方程求解即可
的方程求解即可
(1)证明:设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 为正方形.
为正方形.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 为
为![]() ,
,![]() 的交点,
的交点,
∴![]() 为
为![]() 的中点,即OE为三角形BPF的中位线
的中点,即OE为三角形BPF的中位线
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又因为![]() ,所以过
,所以过![]() 分别作
分别作![]() ,
,![]() 的平行线,分别以它们作为
的平行线,分别以它们作为![]() 轴,
轴,
以![]() 为
为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
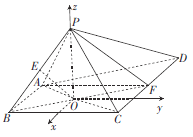
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
假设线段![]() 上存在一点
上存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
设![]() ,则
,则![]() ,
,
即![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则 ,即
,即![]() .
.
取![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,令
,令![]() ,
,
得![]() ,
,
化简并整理得![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.
所以,当![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】商品的销售价格与销售量密切相关,为更精准地为商品确定最终售价,商家对商品A按以下单价进行试售,得到如下数据:
单价x(元) | 15 | 16 | 17 | 18 | 19 |
销量y(件) | 60 | 58 | 55 | 53 | 49 |
(1)求销量y关于x的线性回归方程;
(2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每件商品A的成本是10元,为了获得最大利润,商品A的单价应定为多少元?(结果保留整数)
(附: ,
,![]() .(15×60+16×58+17×55+18×53+19×49=4648,152+162+172+182+192=1455)
.(15×60+16×58+17×55+18×53+19×49=4648,152+162+172+182+192=1455)
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年 份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额(万元) | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长(万元) | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)请用最小二乘法求出y关于x的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额是8万元,估计该公司在该年的年利润增长是多少?(结果保留2位小数)
(2)现从2012—2018年这7年中抽取2年进行调查,记![]() =年利润增长-投资金额,求这两年都是
=年利润增长-投资金额,求这两年都是![]() >2(万元)的概率.
>2(万元)的概率.
参考公式:回归方程![]() 中,
中, 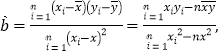
![]()
![]()