��Ŀ����
����Ŀ��ij��˾Ϊ���������2012����2018��ÿ����������ڵĸĽ�����Ͷ�ʣ�Ͷ�ʽ�����������������������±���
�� �� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
Ͷ�ʽ���Ԫ�� | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
��������������Ԫ�� | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
��1��������С���˷����y����x�Ļع�ֱ�߷��̣����2019��ù�˾�ƻ����������ڵĸĽ���Ͷ�ʽ����8��Ԫ�����Ƹù�˾�ڸ���������������Ƕ��٣����������2λС����
��2���ִ�2012��2018����7���г�ȡ2����е��飬��![]() =������������Ͷ�ʽ��������궼��
=������������Ͷ�ʽ��������궼��![]() >2����Ԫ���ĸ���.
>2����Ԫ���ĸ���.
�ο���ʽ���ع鷽��![]() �У�
�У� 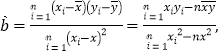
![]()
![]()
���𰸡���1��![]() ��11.43����2��
��11.43����2��![]()
��������
��1�����������ƽ�����ͻع�ϵ����д���ع�ֱ�߷��̣����÷��̼���x��8ʱ![]() ��ֵ���ɣ�
��ֵ���ɣ�
��2����2012��--2018����7��ֱ�Ϊ1,2,3,4,5,6,7�����������оٳ������ܵĻ����¼����ҵ����������ĸ�����������ʼ��ɣ�
��1��![]() ��
��![]() ��
��![]() ��
��
��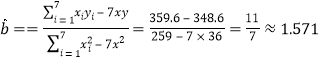 ��
��
![]() ��
��
��ô�ع�ֱ�߷���Ϊ��![]()
��![]() ���뷽�̵�
���뷽�̵�![]()
�����Ƹù�˾�ڸ����������������ԼΪ11.43��Ԫ.
��2���������֪��
��� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| 1.5 | 2 | 1.9 | 2.1 | 2.4 | 2.6 | 3.6 |
��2012��--2018����7��ֱ�Ϊ1,2,3,4,5,6,7�����ܻ����¼�Ϊ����1,2������1,3������1,4������1,5������1,6������1,7������2,3������2,4������2,5������2,6������2,7������3,4������3,5������3,6������3,7������4,5������4,6������4,7������5,6������5,7������6,7��������21�ֽ����
ѡȡ�����궼��![]() ��Ԫ�����Ϊ����4,5������4,6������4,7������5,6������5,7������6,7������6�֣�����ѡȡ�����궼��
��Ԫ�����Ϊ����4,5������4,6������4,7������5,6������5,7������6,7������6�֣�����ѡȡ�����궼��![]() ��Ԫ�ĸ���
��Ԫ�ĸ���![]() .
.

 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�