题目内容
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
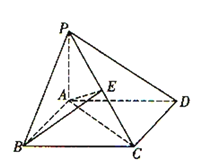
下列四个结论:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正确的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
在![]() 中,由余弦定理可求出
中,由余弦定理可求出![]() ,再由PA⊥平面ABCD,可证出AB⊥平面PAC,再由AE⊥PC于E,线面垂直的判定定理,可证明PC⊥平面ABE,根据线面垂直的判定,可证出BE⊥PC,因此可知正确命题的个数.
,再由PA⊥平面ABCD,可证出AB⊥平面PAC,再由AE⊥PC于E,线面垂直的判定定理,可证明PC⊥平面ABE,根据线面垂直的判定,可证出BE⊥PC,因此可知正确命题的个数.
已知![]() 由余弦定理可得
由余弦定理可得![]()
![]() ,所以
,所以![]()
![]() ,即
,即![]() ①正确;
①正确;
由![]() 平面ABCD,得
平面ABCD,得![]() ,所以
,所以![]() 平面
平面![]() ,②正确;
,②正确;
![]() 平面
平面![]() ,得
,得![]()
![]() ,又
,又![]() ,所以
,所以![]() 平面ABE,③正确;
平面ABE,③正确;
由![]() 平面ABE,得
平面ABE,得![]() ,④正确,
,④正确,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目