题目内容
【题目】设数列![]() 是公比大于
是公比大于![]() 的等比数列,
的等比数列,![]() 是其前
是其前![]() 项和,已知
项和,已知![]() ,且
,且![]() 构成等差数列
构成等差数列
(1)求数列![]() 的通项;
的通项;
(2)令![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)依题意,利用等差数列的性质,解关于a2的方程可得a2=2,设数列{an}的公比为q,
继而可求得q1=2,从而可得数列{an}的通项公式;(2)由(1)知an=2n﹣1,依题意知bn=2n﹣1log22n=n2n-1,利用错位相减法即可求得数列{bn}的前n项和Tn.
(1)由已知得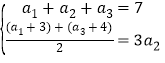 解得a2=2.
解得a2=2.
设数列{an}的公比为q,由a2=2,可得a1=![]() ,a3=2q.
,a3=2q.
又S3=7,可知![]() +2+2q=7,即2q2﹣5q+2=0,
+2+2q=7,即2q2﹣5q+2=0,
解得q1=2,q2=![]() .由题意得q>1,
.由题意得q>1,
∴q=2,∴a1=1,∴an=2n﹣1.
(2)由(1)知,bn=2n﹣1log22n=n2n-1,
故Tn=(1![]() +221+322+…+n2n-1),
+221+322+…+n2n-1),
2Tn=121+222+323…+(n﹣1)2n-1+n2n),
两式相减,可得﹣Tn=(1+2+22+23+…+2n-1﹣n2n)
=![]() ﹣n2n
﹣n2n
=2n﹣1﹣n2n,
∴Tn=![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】伴随着智能手机的深入普及,支付形式日渐多样化,打破了传统支付的局限性和壁垒,有研究表明手机支付的使用比例与人的年龄存在一定的关系,某调研机构随机抽取了50人,对他们一个月内使用手机支付的情况进行了统计,如下表:

(1)若以“年龄55岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用手机支付”与人的年龄有关;
的把握认为“使用手机支付”与人的年龄有关;

(2)若从年龄在![]() ,
,![]() 内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为
内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为![]() .
.
①求随机变量![]() 的分布列;
的分布列;
②求随机变量![]() 的数学期望.
的数学期望.
参考数据如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考格式:![]() ,其中
,其中![]()