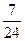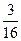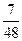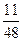题目内容
在球内有相距1 cm的两个平行截面,截面面积分别是5π cm2和8π cm2,球心不在截面之间,求球面的面积.
球的表面积是36π cm2.
已知截面面积,也就能求出截面半径.要求球的面积,只要求出球的半径即可.设球的半径为R,利用几何关系,容易得到球心到两截面的距离分别为 和
和 ,由于球心不在截面之间,即两截面在同一侧,故这两个距离相减即得到两平面之间距离.
,由于球心不在截面之间,即两截面在同一侧,故这两个距离相减即得到两平面之间距离.

如图,圆O是球的大圆,A1B1、A2B2分别是两条平行于截面圆的直径,过O作OC1⊥A1B1于C1,交A2B2于C2.由于A1B1∥A2B2,所以OC2⊥A2B2.由圆的性质可得,C1和C2分别是A1B1和A2B2的中点.
设两平行平面的半径分别为r1和r2,且r1<r2,
依题意πr12=5π,πr22=8π,∴r12=5,r22=8.
∵OA1和OA2都是球的半径R,
∴ ,
, .
.
∴ .
.
解这个方程得R2=9,∴S球=4πR2=36π(cm2).
∴球的表面积是36π cm2.
 和
和 ,由于球心不在截面之间,即两截面在同一侧,故这两个距离相减即得到两平面之间距离.
,由于球心不在截面之间,即两截面在同一侧,故这两个距离相减即得到两平面之间距离.
如图,圆O是球的大圆,A1B1、A2B2分别是两条平行于截面圆的直径,过O作OC1⊥A1B1于C1,交A2B2于C2.由于A1B1∥A2B2,所以OC2⊥A2B2.由圆的性质可得,C1和C2分别是A1B1和A2B2的中点.
设两平行平面的半径分别为r1和r2,且r1<r2,
依题意πr12=5π,πr22=8π,∴r12=5,r22=8.
∵OA1和OA2都是球的半径R,
∴
 ,
, .
.∴
 .
.解这个方程得R2=9,∴S球=4πR2=36π(cm2).
∴球的表面积是36π cm2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
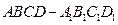 的棱长为
的棱长为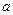 ,它的四个互不相邻的顶点
,它的四个互不相邻的顶点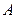 ,
,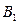 ,
,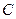 ,
,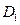 构成一个正四面体的顶点,求这个正四面体的体积.
构成一个正四面体的顶点,求这个正四面体的体积.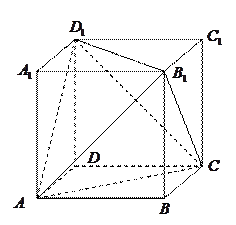
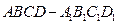 是一个棱长为1的正方体,
是一个棱长为1的正方体,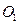 是底面
是底面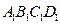 的中心,
的中心,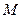 是棱
是棱 上的点,且
上的点,且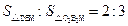 ,则四面体
,则四面体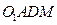 的体积为 ( )
的体积为 ( )