题目内容
若f(x)=ax4+bx2+c满足f′(1)=2,则f′(﹣1)=( )
| A.﹣4 | B.﹣2 | C.2 | D.4 |
B
解析

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设曲线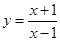 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线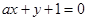 垂直,则
垂直,则 的值是
的值是
| A.2 | B.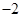 | C.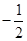 | D.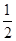 |
函数y=x2cosx的导数为( )
| A.y′=x2cosx-2xsinx | B.y′=2xcosx+x2sinx |
| C.y′=2xcosx-x2sinx | D.y′=xcosx-x2sinx |
由曲线 ,直线
,直线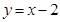 及
及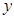 轴所围成的图形的面积为
轴所围成的图形的面积为
A.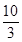 | B.4 | C.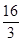 | D.6 |
已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
| A.?x0∈R,f(x0)=0 |
| B.函数y=f(x)的图象是中心对称图形 |
| C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 |
| D.若x0是f(x)的极值点,则f′(x0)=0 |
由直线 与曲线y=cosx所围成的封闭图形的面积为( )
与曲线y=cosx所围成的封闭图形的面积为( )
A. | B.1 | C.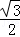 | D. |
己知f(x)=xsinx,则f′(π)=( )
| A.O | B.﹣1 | C.π | D.﹣π |
若函数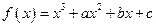 有极值点
有极值点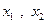 ,且
,且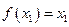 ,则关于x的方程
,则关于x的方程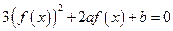 的不同实根个数是( )
的不同实根个数是( )
| A.3 | B.4 | C.5 | D.6 |
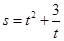 (
(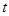 是时间,
是时间,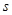 是位移),则物体在时刻
是位移),则物体在时刻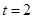 时的速度为( )
时的速度为( )