题目内容
函数 在区间
在区间 上的最小值为( )
上的最小值为( )
A.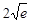 | B. | C. | D. |
D
解析试题分析:由题意,得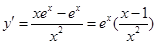 ,所以当
,所以当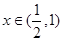 时
时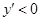 ,当
,当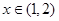 时
时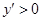 ,所以函数
,所以函数 在
在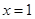 处取得最小值,且最小值为
处取得最小值,且最小值为 ,故选D.
,故选D.
考点:利用导数求函数最值.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
设函数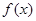 在R上存在导数
在R上存在导数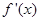 ,对任意的
,对任意的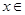 R,有
R,有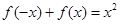 ,且
,且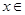 (0,+
(0,+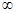 )时,
)时,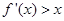 .若
.若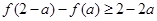 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
| A.[1,+∞) | B.(-∞,1] | C.(-∞,2] | D.[2,+∞) |
定积分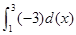 等于( )
等于( )
| A.-6 | B.6 | C.-3 | D.3 |
已知 是可导的函数,且
是可导的函数,且 对于
对于 恒成立,则( )
恒成立,则( )
A. |
B. |
C. |
D. |
函数y=x2cosx的导数为( )
| A.y′=x2cosx-2xsinx | B.y′=2xcosx+x2sinx |
| C.y′=2xcosx-x2sinx | D.y′=xcosx-x2sinx |
函数y=f(x)在定义域(-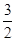 ,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )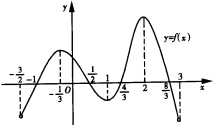
A.[- ,1]∪[2,3) ,1]∪[2,3) | B.[-1,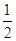 ]∪[ ]∪[ , ,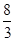 ] ] |
C.[-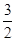 , ,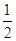 ]∪[1,2) ]∪[1,2) | D.(-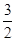 ,- ,-  ]∪[ ]∪[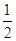 , , ]∪[ ]∪[ ,3) ,3) |
由曲线 ,直线
,直线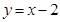 及
及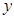 轴所围成的图形的面积为
轴所围成的图形的面积为
A.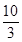 | B.4 | C.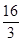 | D.6 |
已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
| A.?x0∈R,f(x0)=0 |
| B.函数y=f(x)的图象是中心对称图形 |
| C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 |
| D.若x0是f(x)的极值点,则f′(x0)=0 |
己知f(x)=xsinx,则f′(π)=( )
| A.O | B.﹣1 | C.π | D.﹣π |