题目内容
20.写出与下列各角终边相同的角的集合,并判断它们分别为第几象限的角.(1)65°;
(2)120°;
(3)-125°;
(4)300°.
分析 根据角终边相同的关系进行判断即可.
解答 解:(1)与65°终边相同的角的集合为{α|α=k360°+65°,k∈Z},
65°为锐角,在第一象限,∴它们为第一象限角.
(2)与120°终边相同的角的集合为{α|α=k360°+120°,k∈Z},
120°为钝角,在第二象限,∴它们为第二象限角.
(3)与-125°终边相同的角的集合为{α|α=k360°-125°,k∈Z},
-125°=-360°+235°,∵235°在第三象限,∴它们为第三象限角.
(4)与300°终边相同的角的集合为{α|α=k360°+300°,k∈Z},
300°在第四象限,∴它们为第四象限角.
点评 本题主要考查角的象限的确定,根据角的范围是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.函数y=cos(x+$\frac{π}{6}$),x∈[0,$\frac{π}{2}$].的值域是( )
| A. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{3}}{2}$,1] | D. | [$\frac{1}{2}$,1] |
5.三点可确定平面的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 1个或无数个 |
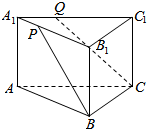 如图,在三棱柱ABC-A1B1C1中,B1P=2PA1,C1Q=2QA1,求证:直线AA1,BP,CQ相交于一点.
如图,在三棱柱ABC-A1B1C1中,B1P=2PA1,C1Q=2QA1,求证:直线AA1,BP,CQ相交于一点.