题目内容
1.若$\sqrt{3}$sinx+cosx=a,在x∈[0,π]上有两个不同的实解x1,x2,则a的范围(1,2)∪(-2,1),x1+x2=当a∈(1,2)时,x1+x2=$\frac{2π}{3}$;当a∈(-2,1)时,x1+x2=$\frac{8π}{3}$..
分析 设函数y1=$\sqrt{3}$sinx+cosx,y2=a,在同一平面直角坐标系中作出这两个函数的图象,应用数形结合解答即可.
解答 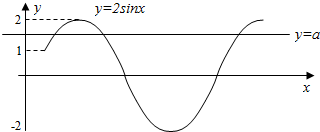 解:设f(x)=$\sqrt{3}$sinx+cosx=2sin(x+$\frac{π}{6}$),x∈[0,2π].
解:设f(x)=$\sqrt{3}$sinx+cosx=2sin(x+$\frac{π}{6}$),x∈[0,2π].
令x+$\frac{π}{6}$=t,则f(t)=2sint,且t∈[$\frac{π}{6}$,$\frac{13π}{6}$]
在同一平面直角坐标系中作出y=2sint及y=a的图象,结合函数的图象可知
当1<a<2和-2<a<1时,两图象有两个交点,即方程$\sqrt{3}$sinx+cosx=a在[0,2π]上有两不同的实数解.
当1<a<2时,t1+t2=π
即x1+$\frac{π}{6}$+x2+$\frac{π}{6}$=π,
∴x1+x2=$\frac{2π}{3}$;
当-2<a<1时,t1+t2=3π,
即x1+$\frac{π}{6}$+x2+$\frac{π}{6}$=3π,
∴x1+x2=$\frac{8π}{3}$.
综上可得,a的取值范围是(1,2)∪(-2,1).
当a∈(1,2)时,x1+x2=$\frac{2π}{3}$;
当a∈(-2,1)时,x1+x2=$\frac{8π}{3}$.
故答案为:(1,2)∪(-2,1).
当a∈(1,2)时,x1+x2=$\frac{2π}{3}$;
当a∈(-2,1)时,x1+x2=$\frac{8π}{3}$.
点评 本题主要考查了辅助角公式在三角函数的化简中的应用及方程的根与函数的交点的相互转化,体现了数形结合思想的应用.

练习册系列答案
相关题目
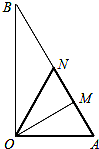 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.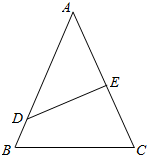 某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.
某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.